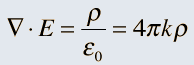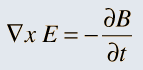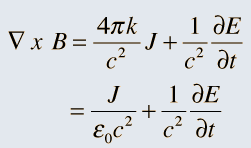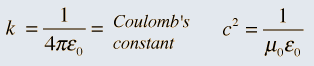|
 |
 |
Volume
6 - Issue 08
AUGUST - 2008 |
IN QUEST OF INFINITY – 18 By Prof. G. Venkataraman
Loving Sai Ram and greetings from Prashanti Nilayam. I wonder whether you recall that towards the end of the last instalment, I mentioned that in the next issue we would be taking a sharp turn. That moment has arrived and I am now going to take you along an entirely different road in our Quest for Infinity. Thus far, I have been telling you many things about the Cosmos, what it contains, how one tries to understand the nature and the structure of the Cosmos, how it might have been born, how it evolved etc. From now on, I shall, for some time at least, be discussing the Principles of Physics that are involved in these investigations. Why do we need to know about the Principles of Physics? That would become clear as we go along. The Heavier They Are, the Same They Fall Let me start with Aristotle, who believed that the heavier an object is, the faster it would fall. In those days, there were no watches, that is to say good timing devices, and hence there was no way this hypothesis could be put to a rigorous test. Intuition suggested that this was the way things were, and that was what Aristotle also believed.
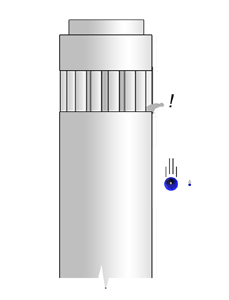
Much later, Galileo, whose name I am sure must be familiar to all of you, questioned this. I am sure you are also aware of the famous experiment attributed to Galileo, which is discussed in the figure below.
Newton’s Great Discoveries While Galileo unquestionably gave us what might be called the cornerstones of Classical Mechanics, it was the famous Newton who achieved the first great leap forward. Newton’s contributions to Physics are absolutely monumental. Today, what Newton discovered is taught even in schools and so many of the present generation might not think much of his contribution. However, the great Chandrasekhar, concerning whom I have said a lot in an earlier issue, rates Newton as the greatest Physicist of the second millennium.
Why is this? For many reasons. Where the science of mechanics is concerned [apart from mechanics, Newton made contributions to many other branches of Physics] Newton not only discovered the famous Laws of Classical Mechanics now named after him [as Newton’s Laws of Motion], but also invented the mathematical tool calculus, that was very much needed for doing practical calculations. [Leibnitz in Germany also developed calculus about the same time, and for a while there was a fierce battle between these two as to who did it first.] Besides giving us the Laws of Mechanics, Newton made another monumental contribution; he discovered the existence of the gravitational force. When gravity was used in conjunction with the Laws of Mechanics, it opened up new vistas in astronomical calculations, which was a huge leap forward. Now while developing his laws, Newton considered the motion of particles that had a mass but no size; that is to say they were supposed to be point particles. However, most of the particles we deal with in Nature have a finite size [at least in the macro world]. So the question arises: “How did Newton get away with it, because the Sun, the Moon, the Earth and so on are all such huge objects?” Newton was able to get away with it all because of the kindness of Nature! You see, all the astronomical objects we normally deal with are usually spherical; maybe they are not perfect spheres, but that does not matter too much. Newton proved that if an object is spherical then it acts like a point mass, at least where mechanics is concerned. To put it more explicitly, a spherical object acts as if it is a point mass with the same mass as the spherical object. Thus, when it comes to discussing ideal trajectories and so forth, one can forget about the big sphere and pretend that it is just a point mass. But caution: One cannot quite get away with it, if one brings in factors like the force that wind might exert on the sphere, whether the sphere is rotating or not, and collisions with an extended object! So you see while one can get away with a lot, the details cannot entirely be swept under the rug. Many have slogged away in precisely those areas but unfortunately, though their work is very useful, they did not quite achieve star status! Sometimes, life does seem to be rather unfair! For a couple of centuries after Newton, Classical Mechanics developed further, with many famous names like La Grange and Hamilton being involved. I obviously cannot go into all those details, and in any event, they do not concern us. It suffices to say the following:
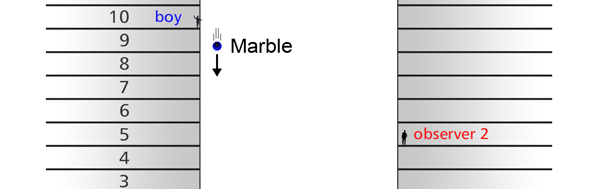
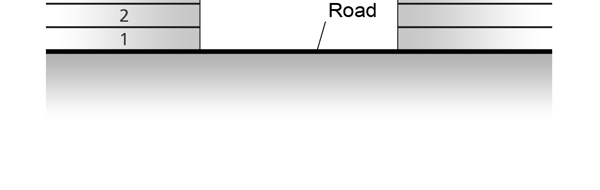
The Invariance Principle Let me spend some time now explaining what is meant by an invariance principle in Physics. In simple terms, it refers to something that remains unchanged, even when we change the perspective. I am sure that statement is as mystifying to you as the word I am trying to explain, and so let go over all this in slightly greater detail. Let us imagine there is a street with multi-storied houses on both sides. Say there is a boy on the balcony of an apartment in the building on the left – see figure below: This boy is on the tenth floor say. There are two people in a building right opposite, that is to say on the other side of the road, and these two people are watching what this boy in doing. One of these observers is, say on the fifteenth floor, while the other is on the fifth. The boy now drops a marble, on to the road; not a good thing to do for the marble could well injure someone walking on the road below; but then boys are boys! This boy drops the marble, and the two observers in the building on the other side are watching. Question: “Suppose these two people are asked to describe what they are seeing, namely the falling of the marble under the influence of gravity. Would they both see exactly the same thing or would what they see be different?”
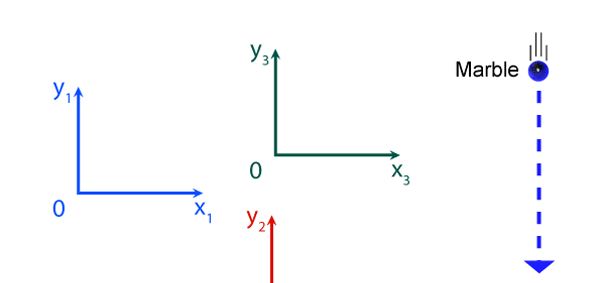
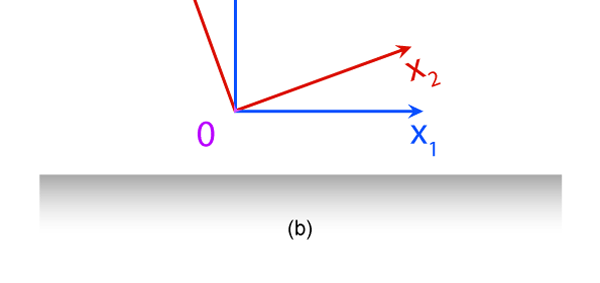
It turns out, and this is what the investigations of people who came after Newton showed, that the mathematical descriptions of the two observations would be identical. Now to describe the trajectory of a moving object, in this case the falling marble, one needs a way in which one can describe the position of the object from instant to instant. The mathematical way of doing this, and that is the best way, is to choose a set of axes, as in the figure below. Having chosen the axes, the position of the particle is then described with respect to these chosen set of axes. In Physics, one refers to this as choosing a frame of reference. Now clearly, when one chooses a set of axes, one must choose an origin; in fact, that is the starting point. The whole point about the boy dropping a marble and two others watching boils down to this: Suppose, a motion is observed and is to be described. Clearly, this requires the observer to choose an origin and specify also a set of axes. Now would the description depend on how the axes are chosen by the observer? Intuition tells us that it should not, but intuition is not always a good guide. There must be sound and logical arguments to make the case. All this was gone through, and nineteenth century physicists concluded that if space is uniform, which it is, then the origin can be chosen anywhere. That is to say, thanks to the uniformity of space, description of motion does not depend on where one locates the origin of the axes. This is referred to as Translational Invariance. By the way, there is also, in many cases a similar freedom in choosing the orientation of the axes; this means, that the basic observations do not depend on how the axes are oriented [one stands up and sees the marble falling, or one could stand on one’s head and observe: results would be the same!]. This is called Rotational Invariance and has deep implications of its own.
Now why did I bring in this invariance business? For the reason that the formulation of Physics based on invariances opens the door to symmetry, and that allows to deduce many general results, otherwise not so easy to obtain. Translational invariance simply means that space looks the same from everywhere. Where Physics is concerned, this is far from a trivial statement. The nineteenth century opened the door to a new way of looking at mechanics, centred around Invariance Principles and symmetry. Translational invariance is connected with a symmetry of Space, and it demoted Space from the Absolute status that Newton had given it, to a lower status. What about Time? That is a different story, to which I shall come a little later. Life is not always all about motion of particles. There are also the phenomenon of heat, light and so on. How did the physics of these subjects develop and evolve? A few words now about that, for that story is also relevant. Understanding the Workings of Heat Let me start with heat. For long, heat was regarded as some kind of [an invisible?] fluid that resided in objects, and heat flow from a hotter to a colder object was simply a case of this mysterious fluid flowing from one object to another. However, there were many unsatisfactory aspects to this hypothesis, and people wanted to see if heat could in anyway be related to the motion of the particles of which matter was made. Of course, this did not happen all of a sudden.
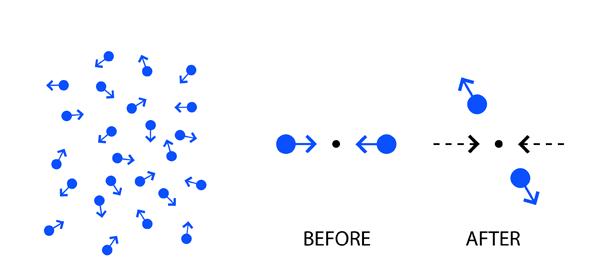
There were what are called gas laws; there were actually two laws, one called Boyle’s Law which is older and the second called Charles Law that came later. These equations represented the behaviour of what was called a perfect gas. Nevertheless, real gases such as hydrogen, oxygen and so on, by and large obeyed these laws, which were referred to as the Equation of State. Basically, they tell us what happens to a perfect gas held in a finite enclosure, like say a balloon or even a hollow metallic sphere. The two gas laws that I just mentioned dealt with macroscopic matter. There was no reference to the fact that matter might be made up of atoms. I must mention that in the middle of the nineteenth century, the chemists were way ahead of physicists in believing in an atomic theory of matter; shame on physicists! But that is a different story and I shall not get into that right now. What happened was that not all physicists were so backward in their thinking about atoms. James Clerk Maxwell of England wondered: “Let me say that matter is made up of atoms. I do not know what exactly these atoms are, but I believe that it is reasonable to assume that hydrogen gas say, is made up a huge bunch of hydrogen atoms, such as the chemists are talking about. Let me next assume that the atoms in a gas move about randomly, and with varying velocities. Since there would be trillions of atoms even in a gas balloon, it is quite likely that often there would be collisions – traffic accidents one might call them! When two atoms collide, I shall imagine that it goes off rather like the collision of two billiard balls. So there are millions of these collisions taking place every second. Surely no one can analyse this vast number of events in detail. But how about talking about certain averages?” Thus Maxwell started asking questions like:
I hope you get an idea of the kind of questions Maxwell was asking. Basically, he was trying to give an atomic theory of gases and in those days, it used to be called the Kinetic Theory of Gases, perfect gases of course. One reason why I am drawing special attention is because I want you to appreciate how while some were looking at generalities like invariance principles, others were thinking in terms of explaining physics on a molecular basis.
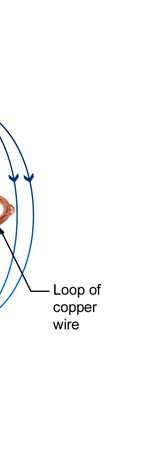
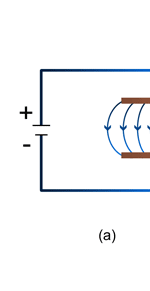
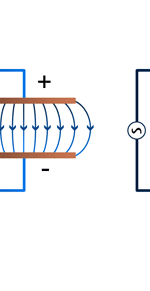
Unifying Light, Electricity and Magnetism Let me move on and turn to another aspect of physics, that which deals with light, electricity and magnetism. If around say 1830 you had told any physicist that all these three were intimately connected, it is more than likely that the physicist would have considered you a fit case for admission into a mental asylum. But you know what? Barely forty or so years later, Maxwell [yes, the same man!] gave an amazing theory that completely unified precisely all these three aspects of physics. This is the famous Electromagnetic Theory, perhaps the greatest triumph of classical physics in the nineteenth century. Commenting on this theory, the incredible Richard Feynman once told his students that centuries from now the world might forget the American Civil War that was fought around the same time, but Maxwell’s Theory would not be forgotten – that shows what a great milestone it was. Now what was the big deal about Maxwell’s Electromagnetic Theory? A few words about that next. You see, for many years, indeed for some centuries in fact, people had bits and pieces of this puzzle related to electromagnetism; but in those distant days, they did not even know that these bits were all part of one big puzzle; that came later. What I am trying to say is that people knew something about static electricity, people knew there were magnetic objects that could attract iron filings and, when suspended, always pointed North, and so on. Soon other interesting things came to be discovered. It was found that a static charge produced an electric field around it, but when the charge was moved, not only did the electric field start varying in time as it should but in addition there now appeared a varying magnetic field. Similarly, when a magnet was kept stationary, it produced a magnetic field in the neighbourhood. However, if the magnet was moved, it induced a current in a wire loop kept nearby. See Figure 5.
So it was clear that electric charge, magnets, electric and magnetic fields and motion of charges as well of magnets were all interlinked. In what way? That was the question that Maxwell answered in 1862, and earned eternal fame. What he gave are referred to as Maxwell’s Electromagnetic Equations.
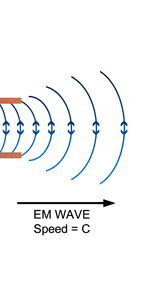
Now one of the great discoveries of Maxwell was that using moving charges, one could actually produce electromagnetic waves; what was even more staggering was Maxwell’s prediction that these waves would travel exactly with the speed of light. At that time, this was an astounding discovery, for it gave the hint that light could indeed be a kind of electromagnetic wave; today of course, every school boy knows that. See figure 6.
The Electrons and The Atomic Plum Pudding Let me now move on to about the end of the nineteenth century, when J. J. Thomson discovered the electron. Thomson suspected that the electron was a constituent of the atom and made up a model of the atom which we in college used to call the ‘bun model’ [in England it was called the ‘plum-pudding model’; we did not know about plum pudding in those days, and so our teacher introduced the model as the bun model!]. I do not know how it is these days but in those days, the bun used to have raisins put in; in the same way, said J.J, the atom was like an object with positive charge in which were embedded the electrons.
Now why on earth did J.J come up with such a picture at all? For a very simple reason. You see the electron is a tiny particle with a certain mass and beside mass it also had negative electric charge. [The electron has a mass of about 9 x 10-28 gm, and one unit of negative electric charge. Its size no one knows exactly, but it is probably as small as 10-16 cm.] J. J then said, I know the electron is a part of the atom; so that means there is negative electric charge in the atom. However, the atom as a whole is electrically neutral. Which means that there must also be positive charge in the atom. How much of positive charge? Just the right amount to cancel all the negative charge being contributed by the electrons in the atom. Now the electron is pretty light; so J.J figured that the mass of the atom must be coming mainly from whatever it was that was carrying the positive charge. Everything put together, led to the model that you see in the figure below.
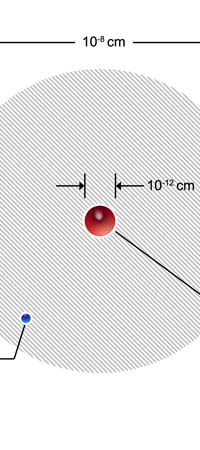
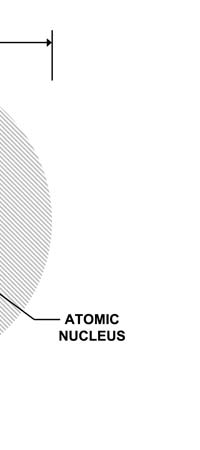
Discovering Nuclear Physics In 1909, Ernest Rutherford working in Manchester University discovered that the positive charge in an atom was not at all spread out like in the Thomson plum-pudding model. Rather, all the positive charge of an atom was concentrated into a very tiny sphere about 10-12 cm in diameter. Now this was an amazing discovery. Why? Because of the following. Let us say we consider the hydrogen atom, the simplest among the atoms found in Nature. This has a size of about 10-8 cm. So, let us imagine the atom to be a sphere of diameter 10-8 cm. In this atom, there is positive charge; that is sitting in a tiny sphere of dia 10-12 cm; that is to say, the positive charge is concentrated in a tiny, tiny region whose dia is one-ten thousandth of the size of the atom. And the mass of the atom, which remember is also associated largely with the positive charge, is located in this minute region. In other words, Rutherford’s discovery demolished the J.J model and gave what was called the nuclear model of the atom, shown below.
So you have this picture: The atom is like a sphere; right in the centre of this sphere, in a very tiny region in fact, are concentrated the entire positive charge as well as the almost the entire mass of the atom. Surrounding this central core region, which, by the way was called the atomic nucleus, was the negative charge in the form of electrons. How many electrons? Just the number required to exactly cancel the positive charge carried by the nucleus. Fine, but where exactly were the electrons? In 1910, this was a million dollar question. Working Out the Inner Picture of the Atom
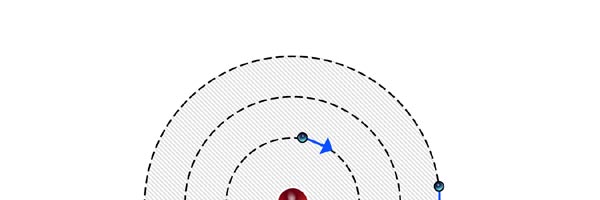
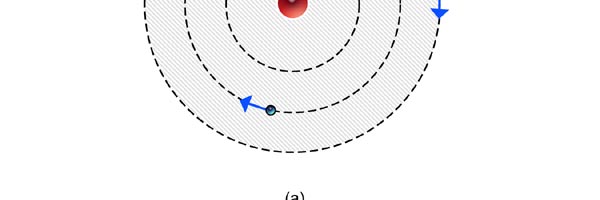
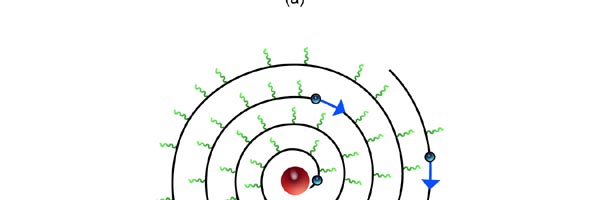
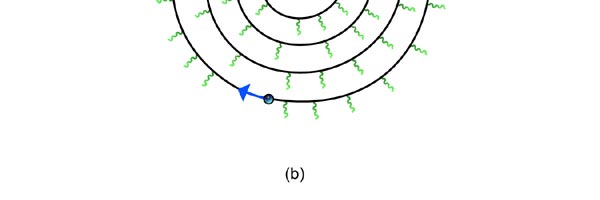
At that time, there came to Rutherford’s lab a young man named Niels Bohr from Denmark. Rutherford said to Bohr, “Why don’t you come up with a working model for the atom?” Bohr said he would try. So the first thing he did was to say, “Well, why not imagine the atom to be a mini replica of the solar system? That is to say, there is the nucleus at the centre, presiding over the atom like the Sun does over the solar system, and the various electrons simply whirl around the nucleus in various orbits like the planets do around the Sun.” This is almost an obvious thing to try, but Bohr found that there was one huge problem with this model. What was that? To understand that, consider a single electron going round a nucleus. See figure 9 below. Now the nucleus is positively charged while the electron, remember, carries a negative charge; and the electron is going round and round the nucleus, rather like what our earth does, going round the Sun. And this precisely is where the problem surfaces. You see, as the electron goes round in its orbit, it experiences acceleration. According to Maxwell’s famous equations, an accelerated charge would emit radiation. Thus, as the electron goes round and round the nucleus, it would go on emitting radiation. When the electron emits radiation, it would lose energy; thus as the electron keeps going round and round, it would keep on losing energy. Using Maxwell’s equations and all that, one can show that as the electron loses energy, the orbit starts shrinking. In other words, the electron orbit would start spiralling inwards and in no time at all, it would collapse into the nucleus, and become one with it. What it means is that the electron disappears! And when it does, the positive charge of the nucleus would decrease by exactly one unit of charge, due to the cancellation produced by the electron. I hope you are getting the picture. Bohr found that one by one, all the electrons would very quickly fall into the nucleus and get annihilated there; it is all like the moths flying into the fire! And soon, there is only the tiny nucleus left, completely without charge of course, because all the positive charge in it would have been exactly neutralised by the electrons that have been captured. In short, the solar model does not work; in no time at all, the “solar system” collapses! Something was horribly wrong somewhere. Where exactly?
Bohr came up with the answer a few years later, and for that momentous discovery that literally turned the tide of Physics, you have to wait till the next issue!
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Vol 6 Issue 08 - AUGUST 2008
|
Best viewed in Internet Explorer - 1024 x 768 resolution. |