|
IN QUEST OF INFINITY – 10
By Prof. G Venkataraman

Previous Articles In The Same Series |
|
|
|
|
|
|
|
|
|
Loving Sai Ram and greetings once again. I wonder how many of you appreciate how far we have “travelled” in our quest for Infinity. Some of you might feel that it seems to be an endless journey. So it might seem but when we come to the “end” of our journey, you would perhaps get a terrific surprise! I don’t want to spoil it for you by telling you something about it right away, but I thought I would provoke you with that remark to launch you on a guessing game!
OK, let’s get down to business and look back for a moment to see how far we have travelled. After “wandering” all over the physical Universe, we realised that we must find out something about how the Universe came into existence. No doubt God created it, but can we, using our [God-given] skills, find out something about the details? That was the exploration we were engaged in, and that revealed to us the following:
- The Universe came into existence with a so-called Big Bang.
- This Big Bang, we can now say with a fair amount of certainty, happened about 13. 8 billion years ago, with a small margin of error of course.
- When the Universe was born, it was incredibly tiny but soon began to grow; this occurred through the expansion of “space-time”. For our convenience, we visualize this as the expansion of a balloon say.
- There is hard experimental evidence for such an expansion, and this was first obtained by Hubble, named after whom there is now a space telescope – every kid these days has heard of the Hubble telescope though few of them might know anything about Hubble himself [see QFI – 02 for a profile of Hubble].
- Careful examination then revealed that about 300,000 years or so after birth, electromagnetic radiation began to fill the entire Universe, and at that time the temperature of this radiation was quite high.
- As the Universe expanded and this radiation had more and more space to occupy, the temperature dropped; today, it is about 2.8° absolute.
- Called the Cosmic Microwave Background [CMB] this radiation was accidentally discovered in the late sixties and constitutes strong evidence [one of them] for the Big Bang.
- Meanwhile, it was found that the current rate of expansion of the Universe was not enough to explain its size, assuming that at birth the Universe has a size of almost zero. This, among other things led to the idea of Inflation, which was given a respectable shape [with many lingering questions though] by Alan Guth.
|
 |
 |
Edwin Hubble |
|
Alan Guth |
- Subsequent studies have shown that Inflation, an event of unimaginable proportions MUST have occurred – at least that is what most believe.
- The above facts related to astrophysics and cosmology have got increasingly connected to the micro world also. First, looking at the radiation from stars, people developed theories about the elemental composition of stars. Then when it came to energy produced by stars and their subsequent fate, people went down to the level of nuclei and even protons and neutrons to discuss the physics of stars.
- Slowly, people have started relating the physics of very small distances to the nature of the very tiny Universe. Just to remind you, for the cosmologist, very small distance means something like 10-30 cm and below, going even as far down as 10-48 cm. Of course, this also means that one is talking of the Baby Universe when it was incredibly young – I have mentioned all this earlier.
The point I want to drive at via the above recap is that we have now begun to seriously connect the Big and the Small. We know that philosophers have been talking about it for a long time. Modern science has successfully linked the seed to the tree and the DNA to the human body. But now, taking a giant leap, man is trying to link the Cosmos at the macro level to the infant Universe, indeed to the instant of Creation. Man is attempting this via the latest developments in the physics of elementary particles. That is roughly where we were last time, and towards the end of that instalment, I was beginning to tell you something about String Theory, the hottest topic in particle physics today. For your convenience, I have given separately in BOX 1, a thumb-nail portrait of String Theory. I strongly urge you to at least glance through this once, so that you may appreciate better what follows.
|
 |
Interacting strings could unite all four forces
(Digital artist's conception) |
|
As described in the box, in String Theory, the starting point is that it is not particles but strings that are basic to the physics of small distances. Although it is yet to hit the headlines in terms of making spectacular predictions that have come true [that is what Einstein’s Theory of Gravitation achieved, way back around 1915-1920; see QFI – 02], String Theory nevertheless has many pluses going for it. These include:
- It is a theory tailored to the world of the very small and based on quantum mechanics, the inclusion of which is a basic and mandatory qualification for any theory to be taken seriously.
- String Theory in its current version, evolved after many modifications and improvements, and is able to accommodate SUSY or Super Symmetry, which allows for a symmetry between quarks and leptons.
- In that sense, String Theory may be seen as a part of the various attempts made during the last few decades to tie up the strong, the weak and the electromagnetic force under one umbrella. For many years, physicists have been searching for such a Grand Unified Theory [GUT] but have not come up with a really good one. String Theory has all the potentialities of emerging as the final winner – that is one more plus for it [in addition to these cited earlier].
- Nasty problems called infinities, have dogged all theories of the world of the small – technically called quantum field theories – and it takes a lot of ingenuity to overcome the difficulties posed by these unwelcome infinites. By comparison, String Theory does not suffer that much from this disease.
- Most importantly, String Theory makes room for gravitation in a natural way. This is a huge bonus because a conventional “marriage” between Einstein’s classical and very powerful theory of gravitation and relativistic quantum mechanics [that came later], a “marriage” that is absolutely mandatory when one enters the world of the small, is next to impossible. That traditional difficulty is overcome in String Theory, almost in passing it seems. It is this very impressive aspect of String Theory that makes it very appealing to many. Incidentally, whereas GUT type theories unify only the strong, the weak and the electromagnetic forces [three out of the four basic forces known], String Theory offers the possibility of bringing all four forces [that is to say the three mentioned above AND gravitation] under one single regime – and that is a real great attraction. If it clicks, String Theory would be the ultimate theory, which is why some tout it as the Theory of Everything [TOE].
|
 |
| |
1-D, 2-D and 3-D strings |
At this stage, I should mention that some daring physicists said, “Why only strings? Why not membranes?” Then a smarter guy said, “Listen, particles can be viewed as zero dimensional strings. The usual string is a one-dimensional string while the traditional membrane [like that in a drum] is a two-dimensional string. Why not three-dimensional or four-dimensional strings? Indeed, why not a n-dimensional string?” Mathematicians are like that! Sometimes they really go wild, but out of such flights of fancy, many discoveries also emerge.
By the way, these multi-dimensional membranes are sometimes simply called branes. So if you want to sound smart and someone is trying to tell you something about String Theory, just put on a wry face and mutter wisely, “Oh, you are talking about branes, are you?” The other person would begin to look at you with respect. [That lesson on one-upmanship comes free, compliments of H2H!] But one thing about String Theory is that it comes with many more dimensions than we are used to and that might make you pretty uneasy, quite legitimately too. More about these extra dimensions next; but meanwhile, if you want to know more about strings, please see BOX 1.
Let me now attend to the puzzling question of extra dimensions. We are supposed to live in a world that is essentially three-dimensional; that being the case, what on earth do these fanciful extra dimensions mean? To answer this question let us go back to Einstein who in a manner started it all, though not with strings. One fine day he said, “Folks, I have news for you. Yes, the world we live in does have three dimensions of space. But you know something? Time is also a kind of dimension and we need to consider time along with space. I therefore propose that we must talk of four-dimensional spacetime rather than merely of three dimensional space.” At that time, Einstein’s pronouncement was a great shock but over a century, we have got used to that idea. In fact, modern satellites cannot work properly if we did not use the big man’s ideas in designing them. I am told that these ideas are used even in the GPS systems now found in many cars!
That’s OK but what about this huge proliferation in dimensions, with people quite comfortably talking about ten and eleven dimensions? Was it not making things unnecessarily complicated? Why all this in the first place? Well, let me tell you that physicists are quite smart and what with all the fierce competition around they would not mess around with higher dimensions [brought in along with strings or branes, call them what you will], unless there was mileage; and there sure was.
|
 |
| |
Albert Einstein |
There is a fairly long history in this business of proliferation of dimensions. As I told you just now, everyone always accepted that we live in a space of three dimensions. In addition to space, there was of course Time, and it was believed till Einstein came along, that space was space and time was time and that the two shall remain distinct. In 1915, Einstein changed all that with his famous theory of Gravitation.
He talked about a unified spacetime rather than space and time separately. Mercifully, this concept of unified spacetime was not normally required except in special circumstances, as for example, when one deals with astrophysical objects.
Around 1919-1920, a young scientist named Kaluza in USSR read Einstein’s by now classic work on general relativity and gravitation. He then said to himself, “Einstein says that gravity is just a manifestation of curvature in 4 D spacetime. Is it possible to understand the electromagnetic force also in the same manner?” After pouring over the problem, Kaluza came to the conclusion that if Einstein’s 4 D space was made 5-D, then both gravity and electromagnetic forces could perhaps be regarded as suitable curvatures of this higher dimensional space.
It was a bold idea, in a sense extending Einstein’s path-breaking concept to a new height. Basically, it was an attempt to see the basic forces in terms of higher dimensions. We must remember that in 1919, only gravitational and electromagnetic forces were recognised as basic forces of Nature; the weak and strong forces operating in the nuclear domain were unknown then.
Kaluza wrote a paper and sent it to the Master for comments. When Einstein received the manuscript, he wrote back:
|
 |
Theodor Kaluza |
|
"The idea that this representation of the electric field can be achieved through a five-dimensional cylinder-world never occurred to me and would seem to me to be altogether new. I like your idea at first sight very much. …. If no apparently and irreparable objection occurs to me when reading your detailed exposition, I will be pleased to present your paper on the subject to the academy here."
Just one week later, Einstein wrote,
"I have read through your paper and find it extremely interesting. Nowhere, so far, can I see an impossibility. On the other hand, I have to admit that the arguments brought forward so far do not appear to be convincing enough."
Cold water for Kaluza! Two years later, however, Einstein changed his mind and wrote as follows:
"I am having second thoughts about having restrained you from publishing your idea on a unification of gravitation and electricity two years ago. … If you wish, I shall present your paper to the academy after all, provided you send it to me."
And that is how Kaluza’s radical idea got the highest blessing, with a delay of two years. I must stress that Kaluza did not unify the gravitational and electromagnetic forces in the way we understand unification of forces now. Basically what he had done is the following: While Einstein gave a geometric way of looking at gravitation, that is as the curvature of 4 D “space”, Kaluza was saying, “Listen, if you make 4 D ‘space’ into 5 D ‘space’, then you can interpret both gravitation and electromagnetism as appropriate curvatures of this 5 D “space”.
|
 |
| |
Oscar Klein |
Einstein’s four-dimensional world based on spacetime made room for a geometric interpretation of gravity, while Kaluza’s extension to five dimensions allowed room for the electromagnetic force to be interpreted in a similar fashion, along with gravity of course.
However, both these descriptions were classical. With the advent of quantum mechanics in the late twenties, Oscar Klein in Sweden wondered how these descriptions would get modified in the quantum picture; and one fine day, Klein came up with an equation which was a five-dimensional extension of what is called Schordinger’s wave equation. This allowed one to engage in a quantum analysis of what happens in a higher dimensional world under the combined influence of gravity and the electromagnetic force.
Kaluza’s extension of Einstein’s idea and its subsequent adaptation to the quantum world by Klein came to be called the Kaluza-Klein theory. It was a nice toy to play with and that was about it; nothing much more came out of it except one interesting idea about what happens to the extra dimension. That is what I shall briefly deal with next, for this idea lingered, for many decades though in limbo, until it became resurrected and found an important role to play.
When Kaluza and Klein started talking of the fifth dimension, people said: “Listen, Einstein has already complicated life by declaring Time to be space-like, married space and time into one entity which he calls spacetime. And now you fellows are talking about a fifth dimension. If this fifth dimension really exists, why on earth don’t we see it or experience it? Where has it hidden itself?” This is an interesting question that played a very useful role by leading to the idea of compactification. The idea behind this so-called compactification is illustrated in the figure below. Basically one says, that the extra dimension “curls” itself so much that at the “practical” level, it appears as if the extra dimension is not present.
|
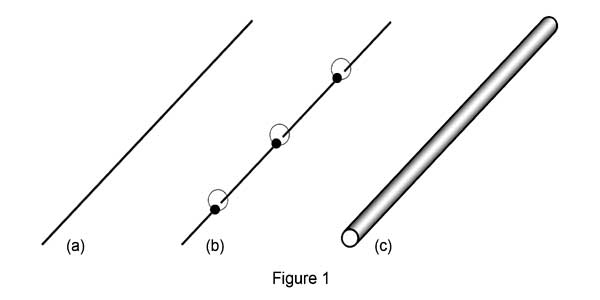
FIGURE: 1 This figure illustrates how one can understand compactification. We start with a line [see (a)]. Suppose we place a circle at every point on the line. In (b) are shown some of these circles. If the line is densely packed with such circles everywhere, we get a tube as in (c). As is evident, the surface of this cylinder is two-dimensional – just cut the tube across and spread it, you get a rectangle instead of a line; that is what I mean by two-dimensional. Imagine now that the radius R of the circle becomes smaller and smaller. The diameter of the tube would then start shrinking and soon, the tube would start looking like a line. This is in terms of appearance only; in actual fact, what appears to be a line would still be a tube, but with a diameter too small for the eye to see. This is what compactification means. |
I hope the figure above makes clear what compactification means. It simply says that the extra dimension is so small that for normal purposes it does not appear to exist, or even if it did, it does not bother us.
Question: “Can the compactified dimension ever make its presence felt? If so, under what conditions? And what on earth does it imply?”
All good questions, which we shall now try and deal with.
Let me start with the first question. The figure above should make it clear that compactification is believed to make the extra dimension so small that it would hardly affect our normal lives. OK, the stock market would not be affected but can this compactified dimension ever make its presence felt? Sure, when we start exploring phenomena at very small scales. How small is small? Maybe around 10-43 cm or so.
Well that takes care of the first of many questions that crop up. Now to the second question: “What do these extra dimensions of String Theory mean? What are they telling us?” That is a tougher question but one can attempt a speculative answer as follows. You see, when Einstein took the first step about a hundred years ago, he essentially said, “You know? If we think of space having four instead of three dimensions as usual [by making time into a “pseudo” dimension if you will], then we can explain gravity by using this “fourth” dimension. Then came Kaluza who said, “Hold on a minute; I think if we go beyond Einstein and add two extra dimensions instead of just one as Prof E did, then we can explain not only gravity but also electromagnetic forces.”
That’s OK but now with String Theories, we have a big proliferation with 10 or 11 dimensions [and maybe even more by come accounts]; what happens now? People are wondering whether the extra dimensions are in any way related to several new and exotic attributes of elementary particles. What I mean is this. When we think of classical particles [I mean like what Newton considered], we would certainly attribute a mass to the particle and also a electric charge if it possessed one. Thus, we would say the proton has a mass of so much and a positive electric charge of one unit. Similarly, the neutron has a mass of so much but has zero electric charge; and so on. However, thanks to intensive investigations in the post-war years, it became clear that elementary particles have all kinds of exotic attributes like spin, colour [in some cases], baryon number and lepton number [as applicable], and so on. All these properties, by the way, are not related to the physical space we live in. Maybe they are related to the extra dimensions coming out of the latter-day exotic theories like String Theory, including various versions of it; that certainly is an interesting guess but we really do not know. I am sure we will hear more on this subject in the years to come; the last word has certainly not been said – that is my impression, and I hope I am correct!
|
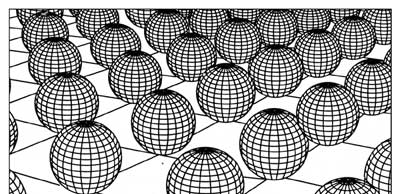
FIGURE 2 This figure seeks to illustrate the concept of (7 + 4 =11) dimensions, of which seven are compactified. Shown here are a set of spheres placed at several points on a plane. The spheres are associated with these points the same way circles were associated with a line in Figure 1. Suppose every point on the plane in this way, then we would have a space that would be 2 + 3. Clearly, we cannot depict such a space since we live in 3 D space. Guided by this figure, one can similarly associate a seven-sphere [sphere in seven dimensions] with every point of 3 D space so that 3 D space becomes 10-dimensional. With time included, 10 dimensions then become 11 dimensions.
This is the way to understand how space as we know it can have many more dimensions that we actually experience. These extra dimensions we do not make any impact on us in our normal life because they have been compactified to a size too small for us to see or experience. Thus, while String theorists need 11 dimensions for developing their theories of the microscopic world, we need not lose any sleep about the extra dimensions they invoke because they are too small as far as we are concerned!
|
To sum up this part of the discussion regarding extra dimensions, I should say the following:
- It now seems inevitable that for getting a complete theory in 4 D [3 space + and time], we have to start with a “parent” theory in higher dimensions. The number of dimensions could be 10, 11, or even higher. The issue does not appear to have been settled yet.
- After the higher-dimensional theory is fully worked out, we must descend to 4 D to make contact with the real world. This calls for compactification of the extra dimensions in a suitable manner and to a suitable size.
- Size of the compact dimensions? No one knows for sure but most guesses are that the size is very small, of the order of 10-43 cm.
- Would all compactified dimensions have the same size or would the sizes be different? No one knows.
- When does compactification occur during the evolution of Universe? No one is sure but it must have been very early, like say around 10-30 sec or so.
- Does the size of the compactified dimension stay constant or vary with time? No one knows for sure, but almost everyone agrees that these compactified sizes remain constant from the moment compactification occurs.
The story of extra dimensions does not quite end here. Strings and branes and their relationship to gravity has led to an interesting idea. To explain this, I must start with the figure below.
|
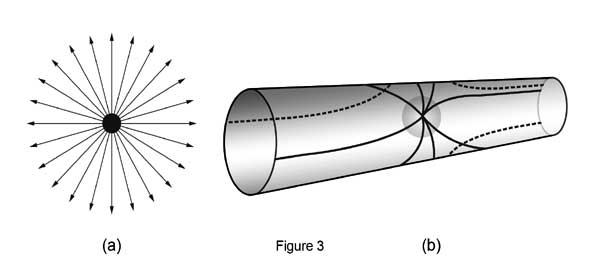
FIGURE 3 This figure illustrates how gravity might operate on different scales of length. (a) shows how the gravity lines of force radiate from a particle in accordance with Newton ’s law, which is OK, especially when the particle is at rest. This radiation pattern is typical of what is called the inverse-square law. That is to say the force is inversely proportional to the square of the distance between the particle and the point where the strength of the force is being measured. This is conventional behaviour. (b) shows something much more complicated though in a schematic manner. Here the cylinder shows a two-dimensional space, of a line plus circles everywhere as I have described earlier.
Let us say there is a particle in this space. In a small region of this 2 D space, around the particle, represented by a small circle, gravity force lines do appear to radiate radially outwards. In other words, in this limited region, the behaviour appears to be Newtonian. However, to infer that the behaviour is Newtonian in this space is wrong. That is what this figure seeks to illustrate. Just follow the lines beyond the small circle. We see then that the lines spread out in a very special way and indeed in some regions the lines are parallel to the axis of the cylinder – very different from radial behaviour you would agree. In other words, in this space as a whole, Newton ’s law does not work!
|
I hope you have studied the figure above. This raises a question. We all assume something taught in high school, namely, the force law in Newton ’s theory obeys the rule:
F is proportional to (1/r2).
Question: “How well has this law been actually tested in the lab?”
The answer is: “At large distances, like over the solar system for example, the law has been tested with fairly high accuracy.” That’s fine but what about small distances? Here the story is: “It has been tested to distances of the order of say a mm or so but lower than that, especially at very small distances, there has been no check.” As a matter of fact, some theorists have suggested that if there are extra dimensions and the extra dimensions are compactified etc., then at small distances in 3 D space, the force law might could behave like
F is proportional to (1/r2+n),
where n is some number. In other words, instead of an inverse square law, gravity might follow an inverse (2+n) law, where n is some number. Reacting to this, some people said, “That’s interesting but not exciting enough; anything really exciting?” It turns out there are many exciting implications if gravity does not follow what Newton thought it did. Let me mention just one of these amazing implications.
Earlier when I introduced strings, I merely said they were quite tiny with incredibly small sizes; I did not specify their shape, except to consider one simple case, that of a straight string. It turns out that strings can be of two basic types, open at both ends or closed into a loop. According to one picture, the string that represents the electron is of the open type while the string that represents the graviton or the quantum of the gravitational field is closed; and this difference has an incredible implication.
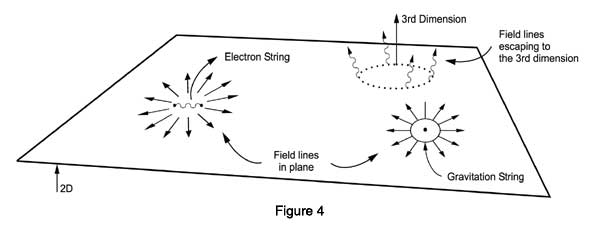
Consider now Figure 4 below, where the electron and the graviton live in a (2 + 1) dimensional world. I have chosen this artificial case just for illustration. A string is a 2 D object and it is easy to depict it on a plane as I have done. The extra dimension is the one that is supposed to get compactified; keep this in mind please. With this simplification, I try to depict the force lines emitting from the electron and the graviton. Now take a close look at the figure.
|
FIGURE 4 This figure illustrates what happens to the force lines emitted by an electron and a graviton, existing in 2 D space, in a Universe which has one more dimension that is compactified. As mentioned in the text, the electron is a string with open ends while the graviton is a loop. Now the interesting thing is that the two ends of the electron are anchored in the 2 D space; which means that they can move about only within the plane, i.e., the 2 D space. The graviton, on the other hand, is not so constrained and can move into the remaining dimension [compactified though it may be for the beings in the 2 D space]. This fact is schematically illustrated here by showing the force lines emanating from the electrons as being confined to the plane while the lines emitted by the graviton radiate not only into the plane but also escape into the other dimension. There is thus an extra freedom that the graviton enjoys and this has deep consequences that are explained in the text.
|
You may think this is all a kind of hocus pocus. Not if you think about it a bit, and to assure that there is a real life analogue to this, I present the figure below.
|
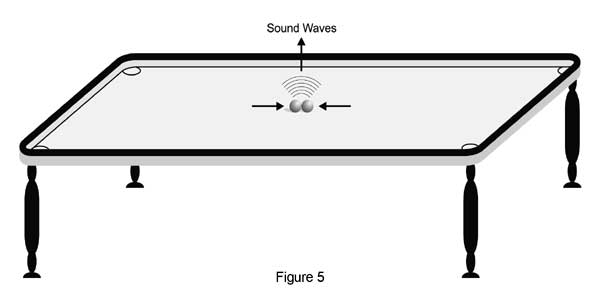
FIGURE 5 This figure offers a simple analogy to illustrate how while the graviton can escape out of the plane, the electron must remain confined to it. What you see here is a billiard table with two colliding billiard balls. Clearly, the balls must move on the table; however, the sound produced by the collision is not confined to the table and can escape into the room; indeed that is how we hear the sound of balls colliding when we watch a billiards game in progress. Now the interesting thing is that whether or not such things happen in particle physics might even be tested soon in Geneva with the world’s biggest particle machine, the LHC getting ready at CERN the European Laboratory for High Energy Physics. Here they would be shooting protons and anti-protons at each other, with these particles not only travelling at nearly the speed of light but also packing an incredible amount of energy. During such collisions, physicists expect the production of mini black holes! And such experiments might indeed reveal whether all this fancy scenario has any basis!
|
To get back to the graviton escaping from the confines of 2 D space, the story does not end with what I have described thus far. Remember I said the graviton would escape from the 2 D world into the third dimension? In terms of the universe we live in, it means that gravitons that rule gravity here can escape from our Universe [of 3 + 1 dimensions] into “another Universe” [!] that is so near yet so far!
Is your head spinning? No wonder! That is the way things work out in this business. Maybe I should not give you more dizziness; why don’t I reserve that for the next issue? OK? Well, so long and take care please! Things are sure going to get curiouser and curiouser as they say! Meanwhile, I urge you once again to reflect for a moment on the amazing beauty and mystery of the Universe we live in.
People say the Universe is an accident. Maybe it is for them; but I find would find it amazing if a whole bunch of molecules got together by accident to form the first living being, descended from which was Shakespeare, who churned out incredible plays, unmatched over five hundred years. Maybe, as Sir James Jeans once said, if we set a million monkeys on a million typewriters and allow them to press the keys, which of course they would do at random, and print out all that is typed, then after millions of years we would end up with all the sonnets of Shakespeare. Some think this might even happen but I tend to feel like Fred Hoyle [a great astrophysicist who actually coined the word Big Bang] did; Fred Hoyle said, “This is about as likely as a tornado sweeping across an auto junk yard, collecting all the bits and pieces lying there and assembling them into a Boeing 737!” The words may not be exact, but the essence is quite close to what Fred said!
As for me, I concur with Gandhi who once began his message with the words, “There is an indefinable mysterious power that pervades everything; I feel it though I cannot see it!”
Think about it!! Good luck and Jai Sai Ram. See you again, and take care.
 |
|
 |
| |
BOX 1- ON STRINGS
Now I offer a brief outline of String Theory as we need to know it. From a historical point of view, the theory has evolved over thirty years in a meandering sort of way, and what I present is a gist of the current picture. As I have indicated elsewhere, there are basically two camps where this theory is concerned. The devotees of one camp are so thrilled that they unabashedly hail it as the Theory of Everything [TOE]! The sceptics, on the other hand, say, “Oh yeah? Well, prove it!”
Now you might wonder how come physicists who are generally very critical of theories unless it passes through fiery tests are willing to shower praise on a theory that has yet to prove itself. Is it some thing like a potential “prodigy”? Is it a case where one side is waiting for the great moment while the other side is waiting for the bubble to burst and TOE to vanish without even a whimper? Time alone would tell; but meanwhile, the excitement is not without reason, and to help you get a glimpse, let me now present a few details of this much-hailed theory in its current Avatar, shall I say?
|
 |
Sir Isaac Newton |
|
For hundreds of years physics has operated on the intuitive assumption that the basic building blocks are particles; this was so in the time of Newton, whose mechanics often assumed even objects like a stone and even the earth could be safely regarded as a particle, when certain aspects of motion were concerned. That is the beauty of physics – to be able to explain complex phenomena with at times amazingly simple assumptions. Once this mountain is crossed, the details earlier glossed over are addressed so as to make the theories and models more realistic.
If Newton thought it convenient to deal with matter as particles when he could get away with it, so did Einstein, when he extended Newton’s mechanics to the realm where speed of objects becomes comparable with the speed of light. [Once again I stress that the size of objects was not forgotten; it was just put away temporarily on the back burner when breakthroughs had to be made – this has always been the case; one step at a time.]
After Einstein, the next big breakthrough in Physics came when quantum mechanics entered the picture – this happened over a period, the first phase of which lasted from about 1924 to 1930. Here too one had to deal with matter, and the basic building blocks were once again regarded as “particles” [although with a dual character – about that, later].
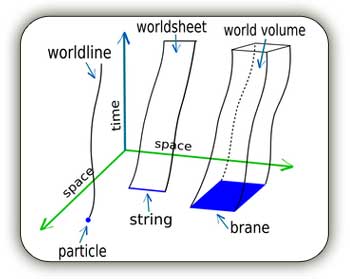
Now what exactly are these so-called particles? This can be understood as follows: Let us start with a short piece of string that is absolutely straight. We assume that the string has no thickness whatsoever; obviously, such a string can never exist but we are talking of an idealised situation. A string of the type just mentioned is said to be a one-dimensional object. Suppose the length of this fictional string is made smaller and smaller, till the length becomes zero. We then have a mathematical point – no size at all! An object of this type but with a mass is what we normally refer to as a particle in physics. In this sense, the mathematical point I just described becomes a string in zero dimensions. The piece of ideal string that I described becomes a string in one dimension; and soon I shall introduce you to strings in higher dimensions.
So you see when physicists started talking of strings instead of particles as they had done for centuries, they were really trying to open new doors. Any mileage in that? Sure! I explain this in greater detail in the main body of this issue but here I would just like to say that when one starts dealing with elementary particles, it is not just the mass of the particle and its electric charge that describe it but may other subtle attributes. For many years, the question was: “Where do these come from?” Additional dimensions provided the clue. I leave those aspects for explanation elsewhere and stay with the main headlines regarding String Theory.
|
 |
| |
Vibrating multi-dimensional strings or BRANES |
Even as the pioneers were exploring various aspects of strings, a few bold [and rash?] physicists said, “Why only strings? Why not membranes?” That was the first step. Soon people began to say, “Why only two-dimensional membranes? Why not membranes in higher dimensions like three, four and so on?”
Thus, people began to talk of “branes” rather than strings! Thus, one had zero dimensional strings, the traditional particles, then the first generation strings in the form of open straight string, curved string and closed loops; after this came strings in 2, 3 and various higher dimensions, all called “branes” for short.
One might ask why physicists did confine themselves to 0-dimensional points for a long time? The answer is that 1-dimensional objects are much harder to work with and often cause technical problems including the violation of special relativity’s mandate that nothing can travel faster than the speed of light.
One fine day when physicists decided to take the plunge and enter the world of strings, they found that the clash with relativity could be avoided by going to higher dimensions. But was this not like replacing one problem with another? Why did physicists waste their time chasing the rainbow as it were? What was there in it for them? That is an interesting point.
You see, physicists are human and they too sometimes ask: “What’s there in it?” Well, before String Theory broke out like a huge rash, many tried very hard to bring together quantum mechanics [QM] and general relativity [GR]. This was a very difficult match making, because in physics, there were no theories so different. QM was non-classical while GR is a classical theory. QM deals mainly with the very small while GR was mostly applied in the realm of the very large and proved itself very successful there.
When it came to the physics of very small distances – and I am here talking of distances like 10-43 cm – clearly, QM cannot be bypassed. Also, since large masses are involved [when one is talking about the Baby Universe] and very small distances, gravity too could not be ignored. So this was a domain where QM and GR had to coexist. Many physicists tried very hard to work out a “treaty” [read quantum theory of gravitation] but it was proving very difficult and it was all very frustrating. That was when string theorists said, “Hey, you know what? Suppose particles were not particles but strings; not just strings in one dimension but in many dimensions; then presto, we are able to predict the existence of the graviton.”
Here I must pause to tell you that graviton is the name given to the basic particle associated with gravitation. The naming has been done by analogy with happened in the case of electromagnetic field, where the quantum was called the photon. The story of the electromagnetic field started in the nineteenth century, as a well-formulated classical theory [due to Maxwell] but in early twentieth century, there came a point when the classical electromagnetic field had to be “quantised”. This could be done by invoking a particle called the photon, the quantum of electromagnetic energy. So by analogy physicists said, “When we succeed in quantising the classical gravitational field introduced by Einstein, we would have a particle called the graviton, which would be the particle of gravitational energy.” And now String Theory was announcing, “Listen guys, we can pull the graviton out of our String Theory!” It was almost like a magician producing a rabbit out of a hat!
So suddenly physicists were saying, “Look, here is a theory that gives you the graviton without all the hassle we faced earlier trying to arrange a shot-gun marriage between QM and GR. OK, we need more dimensions but remember earlier efforts have already signalled that if you want quantum gravity, then you HAVE got to start talking of ten dimensions and the like.” In String Theory that kind of talk is easier; all this plus the stuff about extra dimensions I have presented elsewhere ought to be enough for us here.
I should also mention, that there were many other benefits available from String Theory but before I do that maybe I should clarify what a theory of physics means, and how it is different, if at all, from a model. This is necessary because in physics we have both models and theories. Let me start with familiar things like classical mechanics, relativity, quantum mechanics and so on. What is their status? Now classical mechanics and quantum mechanics provide a general framework, which specify a set of rules according which physics shall be done. I realize this is a very sloppy way of describing things but it adequately captures the spirit of the issue for us.
|
 |
| |
Joseph-Louis Lagrange |
Classical mechanics received a foundation with the pioneering work of Galileo and Newton and was thereafter amplified by many such as Lagrange. Basically classical mechanics is a type of grammar that allows one to calculate how objects move when subjected to a force. This worked fine for a couple of centuries until a few, Einstein in particular, discovered that these rules break down when the speed of the object becomes comparable to the speed of light, classical mechanics beings to fail. How do we know? From experiments. What does that mean? It means that when an object is moving close to the speed of light and one tries to predict the dynamical behaviour of the particle using Newton ’s “grammar”, the predictions do not agree with what is found via experiments in the lab.
New rules had to be developed and the pioneer in that game was Einstein. Einstein did not throw out completely the mechanics developed by Newton and those that followed him. He said, “Newton’s rules work OK when the speed of objects is small compared to that of light. If the speed becomes comparable to that of light, then use my rules. My rules are such that when the speed is small, they automatically give the result that Newton ’s rules give. So my relativistic mechanics is really a super set of Newton ’s mechanics; one may say it is non-relativistic.” In other words, if Newton ’s mechanics is called CM Ver 1.0, then Einstein’s can be called CM Ver 2.0.
Einstein’s path breaking extension came in 1905. But around the same time, some physicists were becoming very curious about the dynamics electrons in an atom would follow. Niels Bohr of Denmark who had moved to England to pursue advanced studies there was one such. He found that when Newton’s mechanics was applied to the electrons in an atom, the predictions went haywire, even if the electron moved at speed much less than the speed of light. In other word, Newton ’s rules were failing not only in the domain of high speeds but also in the domain of very small distances and for a very different reason it seemed. Thus, Bohr laid the foundation for a new mechanics that would be useful in the domain of the small. These developments occurred in a series of path breaking discoveries to which many contributed [these include de Broglie of France, Schrodinger of Austria, Heisenberg of Germany and finally, Dirac of England]. At that point, say around 1928 or so, a new quantum mechanics had been developed, tailored specially for the domain of the small. And then Dirac made one more brilliant leap forward, by bringing Einstein’s relativity and quantum mechanics together into new grammar called relativistic quantum mechanics. This happened around 1930 or so; but all was not over; there were some major glitches still and they got cured later thanks to many people's contributions. However, those matters do not concern us now.
I went into this historical digression because I wanted to draw attention to one important point which is that from around 1950 onwards when particle physics began to gallop, the “grammar” they used was the highly refined and perfected version of quantum mechanics called by pundits as “relativistic quantum field theory”. So if you want to show off a bit and drop technical jargon, then do not forget this phrase – relativistic quantum field theory! It may win for you some young admirers! The most important point that comes out of this is that grammar is different from a model; a grammar gives a set of rules that are applicable under certain conditions. What about a model? There some simplifications are made that lead to a convenient physical picture that is very helpful but without complications.
You might be getting tired of all this apparent rambling and asking yourself, “Why on earth can’t this self-appointed tour guide stick to one direction and take us through, especially since this journey looks like being long?” Valid complaint but you see like every conscientious tour guide who wants to earn his tip, I want to point out all the details of the local landscape and also narrate bits of the local folklore before moving on; you may say it is the Dharma of the tour guide!
More seriously, the point I really wanted to make was that when one assumed that the basic building blocks of matter were really particles [that is, strings in zero dimension], one had, when one tried to build a unified picture within the umbrella strong, the weak, and electromagnetic forces, and using the apparatus of relativistic quantum field theory, a model called the Standard Model.
Now what is a model as compared to a theory? A model is a simplified picture of an actual complex situation that has the merit of describing most of the essential behaviour without unnecessarily complicating matters. Let me give a simple example. Take our earth; you know it is a “ball” about 12,000 km in diameter. For many purposes, one takes this to be a perfect sphere with radius R, where we give a value for R as obtained from experiments. In fact, we do the same for Mercury, Venus, Mars and so on, the various planets in the solar system. Believe it or not, we can, under certain circumstances, make things even simpler and treat all the planets as points and even the Sun itself as just a point, each with an appropriate mass!
This is how high school students are often introduced to the elements of planetary dynamics, and you would be surprised how beautifully this works. Of course, only up to a point. When one becomes fussy, one must take into account the fine print. In the case of the earth, for example, we have to take note of the fact that the earth is NOT a perfect sphere; further, the density of the earth is NOT uniform throughout and so on. When one does very detailed calculations as one has to on many occasions, for example in relation to satellite orbits etc., all this fine print is needed. A model is thus a simplified picture that is good enough for describing most of the essential features, without bothering about the fine print. The fewer the simplifications, the more realistic is the model; keep that in mind please.
The Standard Model that I referred to is a wonderful model, perfected by the involvement of hundreds of physicists from all over the world, and has done remarkably well in the field of elementary particles. Thus, many are quite content with it and do not wish to look beyond. But the fussy ones are not satisfied with yesterday’s triumphs and crave for a theory, which does not keep out gravity, as the Standard Model does, and that is where String Theory gets a lot of mileage. All this lengthy preamble brings to me to what I really want to say. That is the following: Standard Model, wonderful though it is, has about 20 free and adjustable parameters. The Model does not say, “The numerical values of parameters are as follows.”
In physics, one has frequently got to deal with adjustable parameters; conservatives on the other hand, like to keep the number as small as possible. Parameters are like taxes, generally detested! Indeed, some snobs often say, give me ten parameters and I can fit even an elephant.” The idea conveyed is that with a lot of built-in flexibility, the model can be twisted any way to suit any circumstance! This is no doubt an extreme view but shows how at the end of the day, physicists are quite uncomfortable with too many parameters. The situation with the Standard Model is that while there is universal appreciation for the way it has tied up so many diverse facts in particle physics, it has too many parameters for comfort. String Theory pundits said, “Folks, the days of parameter proliferation are over. Here in our new and revolutionary Theory, we have just a parameter or two.”
|
 |
Some say particles are just strings
vibrating in different modes |
|
This economy of parameters was most welcome, at least to the purists, but it came with a price. When the first generation string theorists started actively trying to explain all particles as different “avatars” of the vibrating string, that is to say, the string vibrating in one mode was an electron, the string vibrating in another mode was a proton and so on, there was a new problem. In the course of the calculations, the theorists encountered “negative probabilities”.
Now this is indeed a weird concept. I mean let us say A asks B, “What do you say is the probability that while it is sunny now, there would be rain in the evening?” B might say, “I reckon there is a fifty percent chance,” or something like that. Suppose B says, “You know what? I think there is – 23.4% chance there would be rain.” If B were to say such a thing, A would walk away thinking his buddy has gone bananas! No wonder, for what on earth is the meaning of minus 23.4%? That was the problem here too! But then these wizards working on String Theory said, “Hey wait a minute! You have a problem with negative probabilities? No problem! We can get rid of it by going to higher dimensions like say ten!”
To some of us this might seem too much, like getting rid of one fantasy with another! But then, people struggling with unifying good old quantum mechanics with gravity had already discovered that if at all they wanted to do that, then they would have to make space have 10 dimensions. So the String Theorists picked up courage and said, “Hold on a minute. Don’t get turned off by these extra dimensions. They are actually reminding us about something that people attempting to unify GR with QM had discovered earlier, namely that if gravity and quantum mechanics have to come together, then many more dimensions would be needed. So take the appearance of many dimensions in String Theory as a good sign and press on.”
It is not possible to cover the rich history of the evolution of the String Theory, even if it spans a mere twenty years or so. It is too full of technical details much beyond the reach of all of us, me included. So let me just give the gist, which is as follows:
First, one saw various versions of String Theory, with the author of each version politely signalling that his version was it. The various versions, I should mention, include all sorts of strings, including those of dimensions higher than one, that is to say membranes in various dimensions [ a concept dealt with briefly in the main body of this issue]. After a period during which a lot confusion reigned as to which version is to be preferred, there emerged a package called M theory for short. The grapevine has it that M in M-theory could stand for master, mother, mystery, membrane, magic, or matrix. Some have speculated that the M is actually an upside down W (for Witten, the man who gave M theory a great push; his portrait is presented in BOX 2). The figure below captures the spirit of the current view:
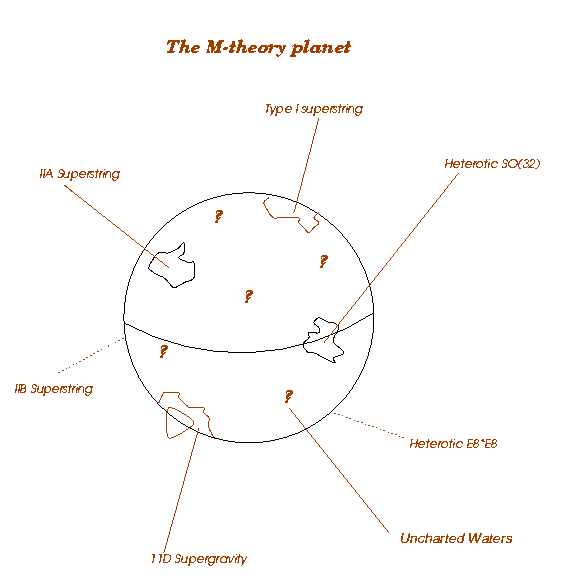 |
This figure is intended to indicate that the world of String Theories can be visualised as a planet [Planet M if you prefer], the different versions churned out thus far being islands and oceans on this planet! This highlights the fact that though superficially the different theories look different, there is an underlying unity. |
M Theory, I should strongly emphasise, is yet to be explored thoroughly and when that happens, a lot more clarity is bound to emerge. But the question still being asked by many sceptics, especially the Standard-Model loyalists, if I might call them that, is: “Well, we agree that there is a lot of fancy mathematics, but physics is all about the real world. What does String Theory, including the much advertised M-Theory version, have anything to say about the REAL world? Has it got any verifiable prediction to offer?” It looks like there might be, but I shall reserve for the next issue. Meanwhile, I feel obliged to say something about Witten, often hailed as the Pope of String Theory. A profile of this amazing man is presented in BOX 2, which follows. |
|
 |
|
 |
 |
|
 |
| |
BOX 2 - ON WITTEN
Edward Witten was born in August 1951 in Baltimore, Maryland, to a Jewish family, the son of Lorraine W. Witten and Louis Witten, the latter a physicist specializing in gravitation and general relativity. Edward received his bachelor’s degree in history (with a minor in linguistics) from Brandeis University.
|
 |
Edward Witten |
|
Witten planned to become a political journalist, and worked briefly for George McGovern’s presidential campaign. He then attended the University of Wisconsin-Madison for one semester as an economics graduate student before dropping out. From politics he returned to academia, enrolling in applied mathematics at Princeton University before shifting departments and receiving a Ph.D in physics in 1976 under David Gross, the Nobel laureate in Physics in 2004.
After completing his PhD, Witten worked at Harvard University as a Junior Fellow and at Princeton as a professor. He was a Professor of Physics at Princeton University from 1980 to 1987. He was also briefly at Caltech from 1999 to 2001. Currently he is the Charles Simonyi Professor of Mathematical Physics at the Institute for Advanced Study in Princeton, New Jersey.
Witten has made several contributions to theoretical physics. Witten's extensive work in the area of theoretical physics has also involved a large number of highly mathematical results. He has been active primarily in quantum field theory and String Theory and in the related areas of topology and geometry.
In 1990, Witten was awarded Mathematics’ most prestigious award, the Fields Medal. Often described as the Nobel of Maths, it is awarded once in four years. Witten became the first physicist to win the Fields Medal. Sir Michael Atiyah said of Witten, "Although he is definitely a physicist, his command of mathematics is rivaled by few mathematicians... Time and time again he has surprised the mathematical community by his brilliant application of physical insight leading to new and deep mathematical theorems... he has made a profound impact on contemporary mathematics. In his hands physics is once again providing a rich source of inspiration and insight in mathematics."
Witten has been honored with numerous awards, including a MacArthur Grant (1982), and the National Medal of Science (2002). In 2006, Pope Benedict XVI appointed Witten as a member of the Pontifical Academy of Science. Witten also appeared in the list of TIME magazine's 100 most influential people of 2004. Since 1992, Witten has been on the board of Americans for Peace Now.
At the time Witten was presented the Field’s Medal [for his contributions to Mathematical Physics], the presenter said:
“Physics was always a source of stimulus for Mathematics so that Mathematical Physics is a legitimate part of Mathematics. In classical time, its connection with Pure Mathematics was mostly via Analysis, in particular through Partial Differential Equations. However, the quantum era gradually brought a new life. Now Algebra, Geometry and Topology, Complex Analysis and Algebraic Geometry enter naturally into Mathematical Physics and get new insights from it.
In all this large and exciting field, which involves many of the leading physicists and mathematicians in the world, Edward Witten stands out clearly as the most influential and dominating figure. Although he is definitely a physicist [as his list of publications clearly shows], his command of mathematics is rivalled by few mathematicians, and his ability to interpret physical ideas in mathematical form is quite unique. Time and again he has surprised the mathematical community by a brilliant application of physical insight leading to new and deep mathematical theorems.
Here is a Q & A session with Edward Witten that gives you a flavour of his tastes and his personality. We don’t say you would be able to understand all that is presented, but at least you would get a glimpse of what geniuses are like. Readers with a physics background may be able to get a bit more.
What is M theory?
M theory is a name for a more unified theory that has the different string theories, as we know them, as limits, and which also can reduce, under appropriate conditions, to eleven-dimensional supergravity. There's this picture that we all have to draw where different string theories are limits of this M theory, where M stands for Magic, Mystery or Matrix, but it also sometimes is seen as standing for Murky, because the truth about M theory is Murky. And the different limits, where the main parameter simplifies, give the different string theories -- Type IIA, Type IIB, Type I, and there's eleven-dimensional supergravity, which turns out to be an important limit even though it isn't part of the systematic perturbation expansion, then there's the E8XE8 heterotic string, and there's SO(32) heterotic string.
So M-theory is a name for this picture, this more general picture that will generate the different limits through the different string theories. The parameters in this picture we can think of being roughly ħ [hbar], which is Planck's constant, and that determines how important the quantum effects are, and the other parameter is α ’ [alpha prime], which is the tension, related to the tension of the string, that determines how important stringy effects are. So traditionally, a physicist looking at Type IIA, for example, by traditional weak coupling methods, explores this little region, and if asked how his theory is related to Type I theory, the answer would have to be, "Well I don't know, that's something else."
And likewise, if you ask this observer what happens for strong coupling, the traditional answer was, "Well I don't know." In graduate courses, you learn that you can do more or less anything for weak coupling, but you can't do anything for strong coupling. What happened in the 90s was that we learned how to do a little bit for strong coupling, and it turned out that the answer is Type IIA at strong coupling turns out to be Type I in a slightly different limit, SO(32) heterotic, and so on. So we built up this more unified picture, but we still don't understand what it means
What is K theory and what does it mean for string theory?
K theory is a mathematical theory that studies topology using matrices, using operators that don't commute with each another. What topology is, first of all, is the branch of mathematics where you don't care about the shape, so for example, a lumpy ball is equivalent to a round ball. But if there are holes, you do care about that, so a donut is different from either of these two. So, mathematicians learned, around 1960, that there was a very powerful tool in topology based on matrices, and that tool was K theory. And since quantum mechanics is about non-commuting operators, or matrices, there has always been a kind of naive analogy between K theory and quantum mechanics. An analogy that seemed naive to most physicists, but was often drawn by mathematicians such as Michael Atiyah.
However, we learned in the last few years that some questions about string theory, but slightly specialized questions usually, are usefully addressed using K theory. What K theory really addresses is a little bit subtle to explain. If you want to understand the charges carried by the D-branes, that's a question that leads to K theory. Or I might say at an even more basic level, D-branes are these strange objects whose positions are measured by matrices, and studying those matrices leads to K theory.
So K theory is the sort of topological underpinning of D-brane theory. But as physicists we're interested very much in whether the ball is round or lumpy, as are different things in physics. We wouldn't want to play baseball with a lumpy ball. So, the topology is just one side of the story.
What is noncommutative geometry and why is it important in string theory?
|
 |
Open and closed strings can be joined in certain ways |
|
Well, one thing which we know about for sure in string theory is that the ordinary classical ideas about geometry are approximations, and don't really work precisely. But what you should really replace them with is not clear. However, there's a naive idea about strings which really only works for open strings.
Open strings are strings with endpoints, like in the original Type I superstring, where a particle was represented by a piece of string with charges at the ends. I've labeled the charges as q and q-bar for quark and anti-quark, but that's modern terminology that might not have been present in the early says of string theory.
Once you've got open strings, they can join together, I'm going to call my open strings A or B, and they join end to end. But there are two ways of joining them. I could join them with A on the left and B on the right, or I could join them with B on the left and A on the right, and I get two different outputs. And it's very much like taking two matrices A and B and multiplying them together. So there's some noncommutativity in the interactions. And when you take account of the fact that string theory is all about geometry, somehow this is geometry where noncommutative objects are built in. In fact I've mentioned now a couple portions of it. There's the noncommutativity of joining strings, and there's the matrices that don't commute, which are related to K theory and also to the D-brane positions and so on.
Anyway, coming back here, you can try to systematically describe open string physics at least in terms of noncommutative ideas introduced in geometry, and you can get a general answer of some kind, but it's rather abstract and very hard to use. However, in the last couple of years, it was discovered that there's a certain limit with a very strong background magnetic field in which things simplify, and you can actually say something simple and useful based on the noncommutative geometry. That's a case where the rather abstract and hard to use noncommutative geometrical concepts actually come down to Earth and become useful.
Why is it so hard to break supersymmetry in string theory?
Well, if I knew the answer, if I knew how Nature has done supersymmetry breaking, then I could tell you why humans had such trouble figuring it out. But I can say one thing about it. When supersymmetry is not broken, it's easy to get a zero cosmological constant in string theory. And although a zero cosmological constant might not be the truth, it's incredibly close to the truth. If you break supersymmetry, if you do it the wrong way, you're going to get a cosmological constant that's much too big, and then you may well get associated problems, such as instabilities, runaways and so on. So it's easy to find ways that string theory could break supersymmetry, but they all have bad consequences. So I assume we're missing something, which is the answer to your question.
How can the cosmological constant be so close to zero but not zero?
I really don't know. It's very perplexing that astronomical observations seem to show that there is a cosmological constant. It's definitely the most troublesome, for my interests, definitely the most troublesome, observation in physics in my lifetime. In my career that is.
What has been the most surprising or interesting thing that you have learned in physics?
I'm going to interpret the question to be what's the most interesting thing I've learned in my career, whether I discovered it or not. It's something I've learned, perhaps through the work of other people or from textbooks. So in that sense, the most surprising thing I've learned, even though I had nothing to do with discovering it, is that strings can describe quantum gravity.
What has been the most surprising or interesting thing that you have learned in science outside of physics?
Well it's not that amazing that to me, a lot of science is physics. So, for example, I can't give you an answer in terms of chemistry, because physics underlies chemistry. I could give you an answer in biology. Biologists have learned lots of wonderful things. But it's hard to properly maintain one's sense of wonder about them, for some things that were known so long that we all remember so little that we take them for granted. But there's the theory of evolution, which is an amazing insight. And there's the understanding of the genetic code, that's a marvelous insight.
Of course, if we move on to math, which you might think isn't physics, but which is much closer to what I know, then there are lot's of fun and exciting things there. I hardly know what to tell you because, again, there are lots of things that are really wonderful but which we take for granted because it's all known. Like there's calculus. Calculus is pretty amazing.
But... it's not the first thing that comes to mind in answering such a question, because such a question tends to make you think of more recent discoveries. But... if I just have to ask, of everything I've ever learned in math, what's the most amazing and surprising -- it might by that calculus should win the prize, even though it's not so new any more. |
|
 |
|
 |

|
 |