IN QUEST OF INFINITY – 09

By Prof. G Venkataraman

---

Previous Articles In The Same Series
Part - 01	Part - 02	Part - 03
Part - 04	Part - 05	Part - 06
Part - 07 Part - 08

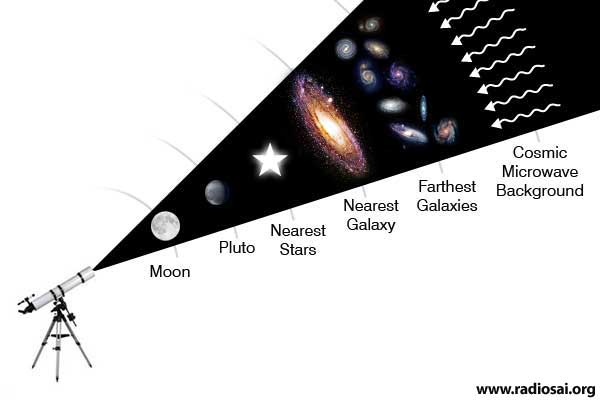
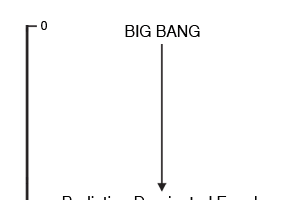
Loving Sai Ram. We resume our joint quest for infinity and before I take you any further, let me look back briefly, to help you appreciate how far we have come. The first stage in our search required us to go back to the time when our Universe was born. How does one go back in Time? We do not have a time-machine that can do that but a simple trick is to look through a telescope. Can one go back in time just by looking? Is that not a crazy idea? So it might seem but actually the idea is not silly, as the figure below would explain.

FIGURE 1: This figure shows how when one looks through a telescope, one peeps deep into space. The more powerful the telescope, the deeper one can peep. All the light we receive comes from distant objects in space. The farther we look, the earlier the light must have started to reach us now. In turn that means that by looking deep enough, we can catch the light that started its journey towards us a very long time ago, bringing information about the early Universe. Of course, to look deep into space, one needs very powerful telescopes. What it all boils down to is, that the more powerful the telescope the farther back we are looking in Time.

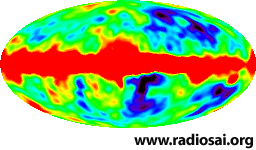
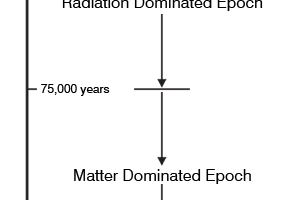
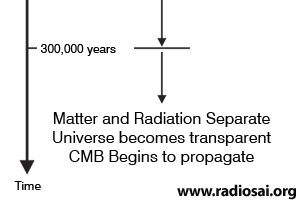
So the first thing we did was to gaze at the wondrous sky above and admiring what fills it. We saw many things, planets, stars, galaxies, exploding stars and whatnot. We pondered and analysed and learnt how galaxies are born, how stars are born, what makes them shine, how they die, how they are reborn and so on [see QFI - 03].

We learnt that simply by gazing at the sky and combining those observations with what physicists were discovering in their labs here on earth, some dared to speculate that the Universe was actually born in a Big Bang. That seemed a great idea, and went very well with an earlier discovery due to Hubble [after whom the Hubble Telescope is named] that our Universe is not static but actually expanding.

Contact between physics, astronomy and astrophysics constantly grew, and people wondered whether Big Bang could have any basis at all in physics. Yes it could, and that came via Einstein’s Theory of Gravitation. We saw that while Einstein was actually the first to discover the fact that the Universe might actually have had a beginning, he brushed aside his own discovery because he was steeped in the Maya of those times, according to which, the Universe is neither born nor dies but always is and steady.

Pity we were not able to meet the Prof for if we had, we would have politely coughed and said, “Excuse me Prof, that thing about being neither born nor dying applies to Supreme Consciousness, and not the Universe. In fact the Universe came out of this Supreme Consciousness, that some call the Atma.” But Destiny had willed that Einstein should “goof” and misinterpret his discovery. Thus he promptly disowned his own discovery, later calling it the greatest blunder of his life. As it turned out, his greatest blunder was to disown his discovery!

Anyway, to get on with the revision, sometime after the idea of the Big Bang was proposed, the Cosmic Microwave Background [see QFI - 02] was discovered, that appeared to strongly confirm the Big Bang. The CMB then became a subject for serious investigations and thanks to satellites it could be studied very carefully, with far greater precision than before. These studies opened up many new avenues of thought.

When the CMB was first discovered, there was euphoria all round, but soon people started worrying. They were worried because the intensity of CMB was the same in whichever direction one looked in the sky. Astronomers murmured, “It is nice to know that the CMB is isotropic, but it is too isotropic for comfort. If this is really true, then how come we have galaxies?” We might wonder why on earth these crazy fellows were worried sick when they really ought to be partying and celebrating the discovery of the CMB? Actually, they did party and all that – let me tell you that scientists are second to none in succumbing to all the temptations that ordinary folks yield to; they are no Rishis! – but at the end of the day when they became sober again, they started worrying about unsolved mysteries. It is this worry that propels science!

That was when the astronomers said, “Listen, let us study this CMB more carefully to check how uniform it really is.” So they built satellites, launched them, collected tons of data, patiently analysed them and finally discovered some thing very important. The CMB was not perfectly uniform; it was substantially uniform no doubt but it also had minute ripples.

FIGURE 2: You have seen this figure before; it is repeated from QFI – 08.

We might say, “That’s nice but so what? And by the way, why spend so many millions for finding this? What’s the big deal?” Well, there was a big deal, and I told a bit of that story last time. Basically, these minute ripples revealed two important things: Firstly, it gave a strong hint about how galaxies came to be formed in an otherwise uniform Universe. Scientists said, “Oh yes, the Universe was uniform but here and there, there were ripples in the density; that was enough of a seed to trigger the formation of a galaxy in that neighbourhood.”

The second point about the discovery was that it gave a conformation to the inflation model of Guth, that I you introduced to. If you recall, the Guth model enabled one to understand how uniformity and fluctuations, though minute, coexisted. Guth said that when it was born, the Baby Universe was in fact quite non-uniform; however, one enormous burst of expansion, inflation as Guth called it, made most of the Universe almost uniform, leaving a bit of very tiny ups and downs here and there, and that was enough to drive the formation of galaxies. There were of course other fringe benefits from the discoveries of the COBE and WAMP satellites, that enabled a very fine and detailed study of the CMB; but we shall not go into that.  

Just to remind you, inflation is something really mind-boggling. In about 10^-30 seconds [which means 0.000 {30 zeros}1], the Universe doubled its size 100,000 times. It means the size increased 2x2x…. 100, 000 times! It is hard to imagine what such an expansion means. Imagine two dots that are just one ten-billionth of a metre apart. That is an incredibly small distance. After 33 doublings, the separation becomes about one meter. One metre might not appear very impressive, but hold on. After 75 doublings, the separation is greater than the size of the solar system. After 110 doublings, the separation is about the size of the Milky Way. And so on it goes; an unbelievable magnification! 

OK, so where does all that leave us right now? What are the questions we have to consider next? Before I get on to that, I must also take stock of what we have learnt about the microscopic world; remember, we are trying to connect the macro and the micro, and get some idea of how the seed and the offspring are connected. So, a quick revision now about the micro-world. We saw that as we go deeper and deeper, we find that the building blocks of every level are made up of the building blocks of the next lower level. For example, molecules are made up of atoms, which are smaller than molecules. The important point is with 92 different types of atoms, one can build up billions and billions of different types of molecules. Atoms in turn are made up of the atomic nucleus and electrons. Atomic nuclei in turn are made up of neutrons and protons; protons and neutrons are in turn made up of quarks. Proceeding in this manner we came up to the point where we now believe that basic building blocks of all matter are quarks and leptons, making up two families so to speak [see QFI - 06]. For your ready reference, I am reproducing below a figure you have already seen.

FIGURE 3: This figure too is a repeat and presents the members of the two basic groups, quarks and leptons, that are the basic building blocks, as we understand now. Anything more basic? May be but as of now, people are not betting on it.

Well, there are these particles, and the question now becomes how do they interact with each other? What are the forces that dictate this interaction? I identified four basic forces: They are: 1) gravity, 2) the strong force, 3) the electromagnetic force, and 4) the weak force. I also told you something about “mediator particles” that makes these forces work, and the relative strengths of these four forces as we know today.

FIGURE 4: This figure lists the mediator particles associated with the four basic forces. Also reproduced is a figure [from QFI – 06] that gives you an idea of the relative strengths of the four basic forces. Right now, gravity is a very weak force. Later we shall see that when the Universe was tiny, the four forces competed strongly and gravity was as dominant as the other three.

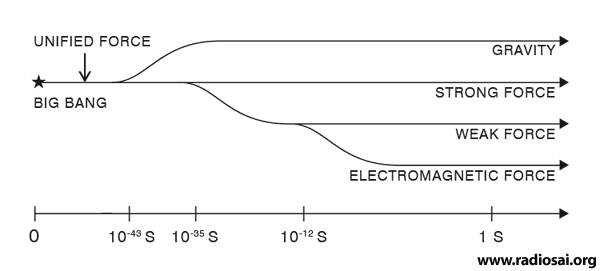
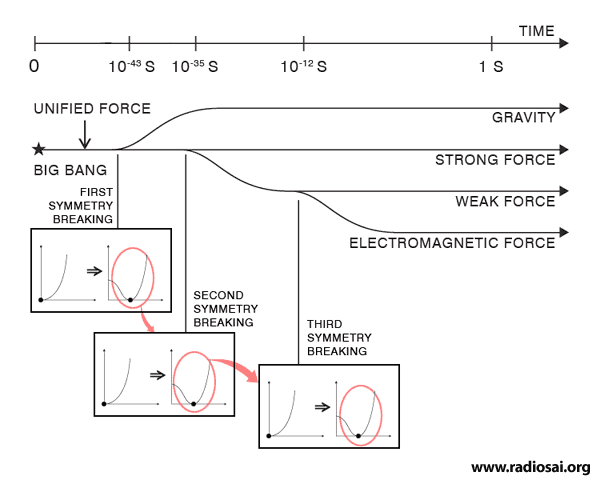
I also pointed out that according to our present understanding, these four forces all come into existence from one primordial force that prevailed at the time of the Big Bang. In this context I presented a figure that I reproduce below.

FIGURE 5: This figure is important and shows how at the beginning of the Universe [read at the beginning of Time], there was only one force, which very quickly became four. Since then, we have been having just these four, and they have influenced the way the Universe expanded and enriched itself, including with the appearance of living matter.

Naturally, the evolution of the Universe, went hand in hand with this one force becoming many. Thus, one could think of several eras, summarised below:

FIGURE 6: Whenever one thinks of long periods of time, one always talks of eras. While history and geology have their own eras, where the Universe as a whole is concerned, the important eras/epochs are the ones shown above.

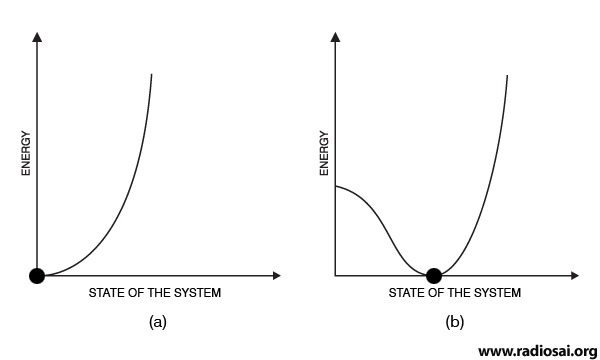
We are now all set to raise the questions that I referred to earlier. There are obviously many questions that could be raised, and here are a few of them:

QUESTION 1: What exactly happened whenever a new force was born [see Fig. 5 above]? What drove the splitting?

The short answer to this question is: Symmetry breaking. This is a very important concept and indeed a corner stone of modern physics. The idea may be understood by considering the solidification of a liquid. As we are all aware, when water is cooled from a high temperature to below 0 degrees Centigrade, it freezes; what we get is ice, which is crystalline. Whereas the liquid is absolutely uniform and homogenous, crystalline ice though very geometric, is actually “grainy” compared to water. We say that this “graininess” is due to “loss of symmetry” and that solidification occurs because of “symmetry breaking”. I know I have greatly slurred over a beautiful [but technical] point but that is enough for the present. With this background, we may rephrase the question posed above: “Can one understand the change from one state to another in terms of symmetry breaking?” Yes we can, and that is what I shall now consider.

In discussing the point we are now considering, we must first note that physical systems always like to be in the lowest possible energy state. Sometimes, they may be prevented from doing so by some constraint [constraint is a check; in real life for example, the parents of a girl might not like their daughter getting married to a certain chap!]; but given a chance, a system would seek that state which has the lowest energy. Keep this important guiding principle in mind.

Now let us look at the figures presented below.

FIGURE 7: These curves show how the energy of the system varies with the “state” of the system. Nature is such that systems always choose that state which has the lowest energy. Curve (a) is typical of water [above the freezing point], while curve (b) applies to ice [produced when water is cooled below the freezing point]. Note that in (b), the minimum energy state [i.e., the state with zero energy] is different from that in (a); it is this difference that drives freezing. Later, we shall use the word order parameter, which is more precise while charactering different “states”.

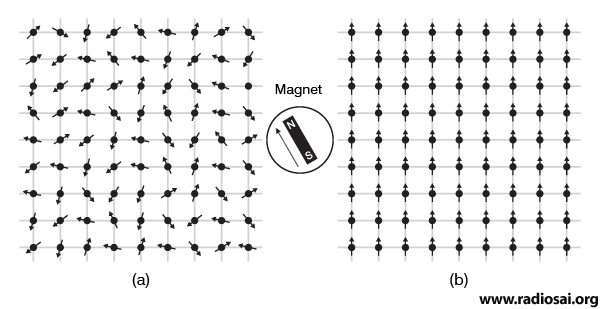
QUESTION 2: How does a curve of type (a) switch over to a curve of type (b) when temperature is lowered below the freezing point? That is left as a puzzle!  

We have two curves here. Let us start with curve (a). It represents the energy curve for the liquid. The x-axis specifies the “state” of the system. The point x = 0 corresponds to the ideal liquid state; and this also happens to be the state of lowest energy. Hence, if the temperature is right [and for water, any temperature above 0 degrees Celsius is favourable for existence as a liquid], the state of minimum energy is clearly the liquid state. When we consider a temperature below the freezing point [equal to 0 degrees Celsius in the case of water], the curve changes to the shape indicated in (b).

Notice that that the energy is zero not corresponding to the state that applied above 0°C but at a different point [representing a different state]. Till zero degrees Celsius is reached, the preferred state is liquid, but when the temperature is lowered below zero Celsius, something happens. That is because the system always seeks the state of lowest energy. Below 0°C, that state of minimum energy is not a liquid but something else [that of ice]. That is how freezing occurs.

Physicists do not use vague words like ‘state’ and so forth. They instead use the word order parameter.  In the example considered here, for the liquid state, the order parameter has a value equal to zero while for the crystalline state, the order parameter is non-zero. The connection between symmetry, symmetry breaking and order parameter is very important and maybe I should digress a bit to explain what it is all about. This is best done by considering a magnetic substance like iron.

Iron is made up of iron atoms and the interesting point is that every atom is like a tiny magnet. Imagine the magnetic atom to be like an arrow, pointing in a certain direction. If you take a lump of iron, the question now is in which direction will the different arrows point? That depends on the temperature of the lump. If it is above 770°C, then the arrows would all point randomly; if, however, the temperature is below 770°C, then the arrows all point in the same direction, as illustrated below.

FIGURE 8: This figure illustrates the concept of order-disorder in magnetic solids. In both (a) and (b), we have a schematic depiction of [crystalline] iron via an array of arrows arranged on a [2D] lattice. The arrows here are symbolic of the fact that every iron atom is a tiny magnet. The way the arrow points is representative of the way the elementary magnets point [see inset in (a)]. The difference between the two figures is in the way the arrows point on the whole. In (a), the arrows point randomly, representing magnetic disorder, the state that prevails above 770°C. In (b), the arrows all point in one common direction, indicative of magnetic order [the state that prevails below 770°C. The critical temperature, namely 770°C, marks the order-disorder transition temperature for iron.

The change from a state when the atomic magnetic point randomly to the state when they all point in the same direction is called a phase transition. When the tiny magnets point randomly, obviously there is no magnetic order but when they all point in the same direction, there is magnetic order. In the state when there is no magnetic order, the order parameter has a value equal to zero, while when magnetic order is established, the order parameter assumes a non-zero value. So we have this rule: High temperature state, no order, and order parameter equals zero; low temperature state, there is order, and order parameter has a value that is non-zero.

OK, all this is fine but where do symmetry and symmetry-breaking come into all this? That is what I shall now briefly describe. Just take a look at the figures below.

FIGURE 9: The figures here are meant to illustrate the important idea of symmetry-breaking. Case (a) deals with the disordered state of iron while case (b) deals with the ordered state. Consider first (a). Imagine that the arrow in every lattice site is rotated by the same angle. We describe this by saying that a rotation is performed on the magnetic system. The illustration in (a-i) represents the situation before rotation and that in (a-ii) represents the situation after rotation. When the number of arrows is small, we could of course distinguish the two patterns, but when the number of arrows is large, it is difficult to distinguish the two. Even in a small lump of iron, we would have about 1023 atoms of iron, and in such a case, it is difficult to say by looking at a pattern like (a-ii) whether a rotation has been performed or not, and if so, by what angle. In such a situation, we say there is perfect rotational symmetry, that is the BEFORE and AFTER situations are indistinguishable. This is the concept of symmetry – invariance to a physical operation performed on the system. Turn now the pair in (b). Here, the BEFORE and AFTER situations, illustrated in (b-i) and (b-ii) respectively are clearly distinguishable; we describe this by saying that in this case, magnetic rotational symmetry is broken. Notice that when there is symmetry, there is no order and vice versa. The message we get is: When there is symmetry there is no order; therefore, order parameter is zero. When symmetry is broken, there is order and consequently, order parameter has a value different from zero. Symmetry-breaking is a powerful concept in physics, particularly elementary particle physics.

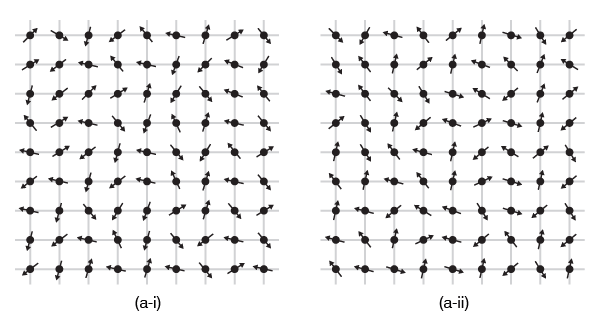
Suppose you take a good look at (a-i). I now ask you to close your eyes, and when your eyes are closed, I rotate the pattern so that it becomes as in (a-ii). Now if we are dealing with trillions of arrows, then it is really not possible to distinguish between (a-i) and (a-ii). One can rotate the first figure by 1 degree, by 42 degrees, 88.4 degrees, or whatever. It makes no difference; one cannot distinguish the unrotated pattern from the rotated one. In such a case, one says there is symmetry, in this case, rotational symmetry. Now look at (b-i) and (b-ii); in this case, it is quite easy to say that the second pattern is definitely rotated compared to the first one. We are able make this distinction because the arrows are all pointing in one direction.

So we get a basic rule [simplified of course]. When there is no order, there is greater symmetry, but when symmetry is lost or broken as physicists say, then there is order. Thus, the symmetry-breaking and the appearance of order go hand in hand. This happens all the time in many physical systems, and thus the study of phase transitions is actively pursued by many. The idea of symmetry breaking [originally applied heavily in the study of solids and liquids] was borrowed by particle physicists to explain some fundamental aspects of microscopic physics. And that part is important for us. How? That is what I shall consider now. Remember the question posed earlier? Let us go back to that.

As a prelude, let us revisit a figure I had presented earlier in QFI - 06. It is reproduced below with some additions.

FIGURE 10: This figure places the time line for the splitting of the original Cosmic force into four distinct forces, along side the energy diagrams associated with symmetry breaking. What this illustrates is how the splitting of the forces is related to symmetry-breaking.

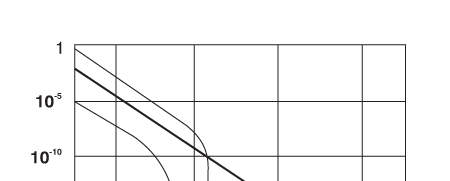
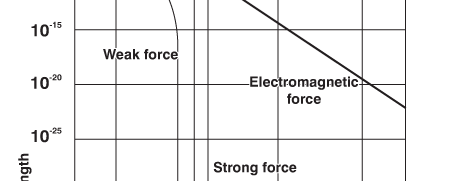
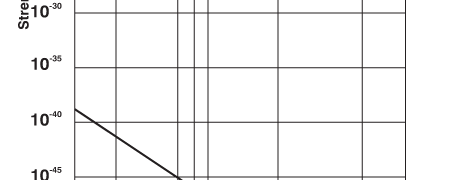
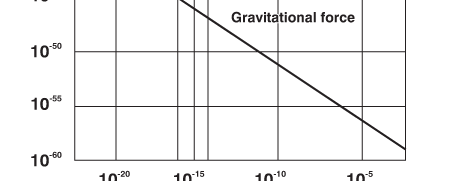
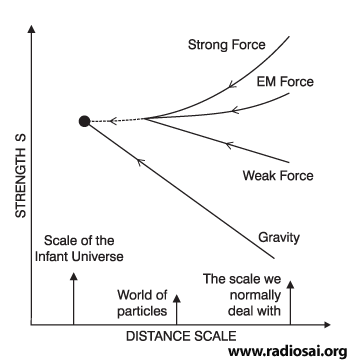
We see that first there was only one force, and then at some time, one force became two. We say one became two as a result of symmetry breaking. The symmetry involved is very subtle, but the basic concept is the same as earlier. In the examples discussed earlier, water to ice and non-magnetic iron to magnetic form of iron, order appeared and symmetry got broken when temperature was lowered. Anything like that operating in this case? Sure. Remember, the temperature of the Baby Universe at birth was astronomically high. As time passes, the temperature falls, symmetry gets broken not just once but many times: thus it is that first one force becomes two, then two becomes three, and finally three becomes four. By the way, many solids show similarly a multiplicity of ordered states, as temperature is varied.

So the important lesson we learn is that the appearance of the four basic forces in a particular sequence has a lot of implications for basic physics, and also of course for the history of the Baby Universe. It is because of this that I have spent a lot of time explaining the basics. By the way, all this is needed to understand some crucial aspects related to inflation; that was also part of the motivation for going into these details. I hope you have not failed to notice in passing how beautifully the Lord has “constructed” the Universe! And you have not heard everything yet!!

On now to the third question:

QUESTION 3: Were the relative strengths of these four forces the same in the Baby Universe also? One can rephrase this question differently; do these four forces maintain their relative strengths, at small distances also, or in other words, do we have to consider different values for the strength of these four forces, when we consider physics at very small distances? 

The short answer to the above question is no; in fact, the relative strengths change as indicated in the figure below:

FIGURE 11: This figure has to be seen along with Fig. 5 presented earlier in this issue. That shows how the effect of the four forces varies with distance in today’s Universe. Let us say there is a number S that proclaims the “strength” of a particular force. We know what the value of S is today, for each of the four forces. Have these values of S remained the same through the history of the Universe? This question when carried over to elementary particle physics becomes: Do the values of S remain the same at very small distances, as they are at larger distances? That is the question answered above. Particle physicists have strong reasons to believe that they do not. There is thus much incentive for physicists to get some idea of the values for S at very small distances. However, the experiments are difficult. Theoretical speculation is, however, possible, and sure enough there is a lot of it. Cosmologists latch on to these numbers churned out by particle physicists, and then try to figure out what might have happened in the early Universe.  That is how the two groups work together.

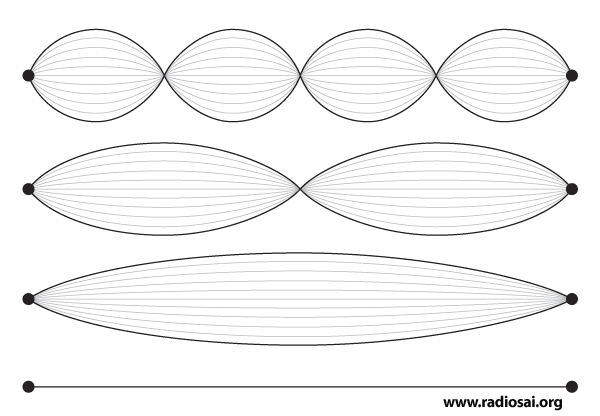
What is particularly striking is not merely that all three of the four forces tend to become almost equally strong but that gravity, which is usually dismissed as a rather weak fellow becomes pretty assertive at very short distances. In other words, gravity becomes a very dominant player when one is considering the Universe at its very early stage. This is a very important point to which I hope to come later. There are two other questions that I shall pose right away and consider the answers later.

QUESTION 4: All earlier discussions of physics treated gravity as if it was a sort of stand-alone thing; is there any way of linking gravity in a natural manner to the elementary particles or the building blocks?

This is a very good and most important question. In recent decades, a connection has been found, and understandably, that is having an amazing and revolutionary impact on physics at small distances and cosmology as well. This is going to engage our attention soon. But meanwhile, let me quickly state the last of the present set of questions.

QUESTION 5: This dark energy, that featured so strongly in an earlier issue [QFI – 08]; how is connected to all this, if at all?

In this issue, I think I can at best barely deal with question 3; the last question I may have to leave for the next time. The link between gravity and particle physics comes via what are referred to as strings.

Time now to talk about strings. Let us go back to Figure 3, which shows the basics as we understand them today. For decades, it has been implicitly assumed that these particles are really particles in the traditional sense. But now there is a strong school of thought that the basic building blocks are strings and not particles, and as a result we now have a vigorous theory called String Theory. That is what I wish to discuss next because String Theory is poised to make a very strong impact and contribution.

The String Theory came into existence almost unnoticed, when a physicist named Veneziano guessed a formula that explained many experimentally observed features related to elementary particles. Shortly thereafter, physicist Nambu in Chicago showed that using Veneziano’s formula is equivalent to treating particles like neutrons and  protons to be different modes of vibration of a string. Now I suppose you are aware that a string clamped at two ends as in the figure below, can vibrate in many modes.

FIGURE 12: This figure shows a vibrating string clamped at both ends. Left to itself, the string would be stationary as at the bottom. When plucked and let go, it can vibrate in many ways; in general, these are combinations of the basic modes of vibration, some of which are illustrated here. In String Theory, the basic idea is that there exist elementary strings and that the so-called fundamental building blocks are just different “modes of excitation” of the string. So, with just one string, one can get different particles! That is just one of the interesting points about String Theory. There are, however, many other compelling features, that have made people take String Theory far more seriously in recent years than they did when it first appeared on the scene.

Developing his speculations further, Nambu argued that if Veneziano’s idea is taken seriously it simply means that many particles known in physics could be simply regarded as one basic string vibrating in different modes. Since that modest beginning, the idea of strings grew slowly at first and then more rapidly, to assume a very strong and respectable position in fundamental physics. How come this has happened? What is it that is going for String Theory? Has it made any sensational predictions that have been verified by experiments? If not, what is so great about String Theory?

Japanese Physicist Yoichiro Nambu		Theoretical Physicist Gabriele Veneziano

Well, basically there are three attractive features about String Theory that cannot be dismissed easily. Firstly, it is less plagued than conventional particle physics is, by a terrible disease called infinities [nothing to do with what we are after!]. That certainly is a blessing that cannot be dismissed. Next, it makes a natural place for a feature called SUSY, which is short for Super Symmetry; I can’t go into that technicality here but SUSY brings quarks and leptons [see Fig. 3] together. SUSY had to be invented and incorporated [by hand, as they say] into traditional particle physics.

In String Theory, SUSY does not have to be put in by hand which certainly is a plus. Thirdly, and this is very important, in String Theory, gravity comes in quite naturally. What I mean is this. In conventional particle physics, one has to say, “Well, we have these particles which interact via many forces, which form a natural part of the theory of particles. However, these particles also interact via gravitational force, but that is not a part of our theory.” In String Theory, gravity does not have to put in by hand, and that is a huge plus.

I must say a few words about the significance of what I have just mentioned. In 1915, Einstein made the spectacular breakthrough that related gravity to space-time and gave it meaning as well as substance. Thereafter, cosmology had a framework for development. And then, in the twenties and early thirties, quantum mechanics came into existence with spectacular success and plenty of mystery. For decades, gravity and quantum mechanics ruled supreme in their own domains – the two did not have to meet, and for a good reason; quantum mechanics was for the microscopic world while gravity became a serious tool when one considered the Cosmos.

Depiction of pulsating, coiling little strings... a theory for the ultimate building block of matter

However, when one began to seriously contemplate on the early Universe, it was necessary for quantum mechanics and gravity to confront each other. One was a classical theory while the other mechanics was the framework that had edged classical physics out of the world of the small. Now they were confronting each other eye-ball to eye-ball, like in a great Western! Was it going to be a great shootout, or was it going to be a mutual compromise with each giving away something? Did it have to be a shotgun marriage? So many questions!

Suddenly, from almost nowhere, String Theory appeared, as a theory based on quantum mechanics, focussed on elementary particles and not on gravity. But unknown to itself, it had left the back door open for gravity to get in and settle into a comfortable relationship with the quantum framework! That is what makes many sit up and take serious notice of String Theory, even though it has still to make spectacular predictions verifiable by experiments. The believers all say, “Making verifiable predictions is just a matter of time. A baby can’t run 100 metres in less than ten seconds. But looking at this baby, we can say that one day this kid is going to do it in 9 seconds!” Will it? No one knows at present. 

String Theory is not yet everyone’s favourite, but its tight mathematics is constantly attracting brilliant minds. Its mathematical beauty has led many to speculate that since it is beautiful, there is a good chance it is true! Sometimes that recipe [mathematical beauty is truth] has worked but other times, Nature has fooled us! Time alone can give us the answer. All this is just the beginning of a very fascinating story.

What more is there? For that you have to wait for the next instalment! Meanwhile, I would like to make only one comment:

The more I see of the amazing manner in which the Universe was brought into existence and allowed to grow, the more does Chapter 10 of the Gita appeal to me. It is all just mind-boggling. In this context, the following quote from one of the poems of William Blake is pertinent. He says:

To see the world in a grain of sand,
And to see heaven in a wild flower,
 Hold infinity in the palm of your hands,
And eternity in an hour.

In the Universe, we have the unbelievable situation of Infinity hiding itself in the smallest conceivable particle [or is it string?]. More about all this next time. Meanwhile, have fun reflecting on all this and the wondrous way in which the Lord works.

Often I recall what Swami once said: “Man knows nothing but pretends he knows everything; God knows everything but acts as if He does not know anything!” If only we spend some time thinking about that! But then we are so frightfully busy, which makes me thank you specially for taking some time off to read this issue. See you again next month. Meanwhile, may God be with you. Good luck and Sairam.

Rock and the World of Science In the September issue of QFI, Prof. Venkataraman posed an interesting question which connected the world of science with the rock and roll scene. It was: “Name a well known rock star who recently completed his Ph. D thesis in astrophysics and submitted it for examination after more than three decades of absence, working in the music world!” The answer is: 'Brian May', the lead guitarist from the very successful group Queen. And here are all the people who sent in the correct replies: Trish Sneddon, USA; Herta Pfeifer, Chile; Soledad Vega, Chile; Chitra Kurup, St.Maarten; Ron Nandha; R Prusty, India; Anuradha Venkateswaran; Sabrina Vharunee, Australia. Well done! - H2H Team

 

---