IN QUEST OF INFINITY – 17

By Prof. G. Venkataraman

---

Previous Articles In The Same Series
Part - 01	Part - 02	Part - 03	Part - 04
Part - 05	Part - 06	Part - 07	Part - 08
Part - 09	Part - 10	Part - 11	Part - 12
Part - 13	Part - 14	Part - 15	Part - 16

Loving Sai Ram and greetings from Prashanti Nilayam. We are almost at the end our tour of the Cosmos, but that does NOT mean we have come to the end our quest. We still have a long, long way to go; more about that later but meanwhile, we do have to address an important question which is: “We have discussed lately, two models for the beginning of the Universe, one based on the by-now-standard Inflation Model, and another which is more a well developed idea rather than a model at present – I am of course referring to the Ekpyrotic Model of Steinhardt and Turok, with which we have been preoccupied in the last few issues of H2H.

As I told you, it would be some time before the mathematics of the Ekpyrotic Model are explored in full detail; right now that appears to be too tough a problem and must await future analysis. But meanwhile, one can ask: “Leave aside all that fancy theoretical stuff. Is there any way hard core experimentalists can give a verdict? They have done this many times in the history of Physics. Can they pull it off one more time, and if so, what does it take?” Well, that is exactly the issue I shall be dealing with this time. As it turns out, God is quite fair! If the task ahead is very difficult for theoretical physicists, it is even more formidable where experimentalists are concerned. That story next!

Going Back in Time at the Speed of Light

Basically we want to know what happened a long, long time ago, almost at the time of the birth of Universe. Now how does one look back in time? We do not have a Time Machine to travel back and forth in Time as H.G. Wells had in one of his famous novels. But there is one clever trick that astronomers have been using for a long time and I have already told you about it. Basically, they say, “Listen, we all know that fast as it is, light does take a certain amount of time to travel; its speed is not infinite; therefore, if we pick up light that left its source say a million years ago, then we can get a glimpse of what happened a million years ago. This is the simplest way of going back in Time and reconstructing the past history of the Universe.”

This is a very important point and we seldom appreciate it. I mean if right now I look at the Sun – not directly of course! – then the sunlight that would be hitting my eyes would actually have left the Sun about eight minutes ago; that is the time it takes for light to travel from the Sun to the Earth. You get the idea, I presume. In this way, if we have very powerful telescopes and are able to pick up light that is very faint – and this is being done all the time – then we can say we are peeping far back in time. The question now becomes: “How far back in time can one go in this manner? Is there any limit or can one go in this manner all the way back to the instant when the Universe was born?”

It turns out that there IS a definite answer which is that at best, we can go back to say about 200,000 or 300,000 years after birth. We CANNOT use this trick for times prior to that. Why? The answer is connected with the fact that almost all of astronomy is done using some part or the other of the electromagnetic spectrum. To put it more simply, when we use an ordinary telescope, we are using ordinary light as a messenger from the past. Instead of visible light, we can use light of longer wavelengths like infra-red radiation, or microwaves, or even radio waves. Or else, we can use electromagnetic radiation of wavelength shorter than visible light, like ultra violet radiation, x rays, or even gamma rays.

Almost 98% of astronomy or perhaps even more, gets done this way. However, electromagnetic astronomy cannot be applied to times prior to about 200,000 years, because the Universe was opaque at that time. That means that electromagnetic messenger waves got absorbed before they travelled far. However, gravity waves of those times could be tapped for information, provided we know how to catch them. Gravitational astronomy has yet to get started because we have not even detected any gravitational wave. In BOX 1, I have explained what exactly is a gravitational wave and therefore I shall not repeat that here. But there are some implications that I shall now point out.

How Mass Affects Space and Time

Let me first take you back a few issues [to QFI 05] when I discussed some of the implications of Einstein’s Theory of General Relativity and Gravitation. I mentioned then that according to this theory, when space-time becomes curved, it implies the existence of a mass. I realise this is a far from adequate way of describing what the theory actually says, but for our purposes, I think it is OK to say when we talk about an object with a certain mass m say, it means that space in the neighbourhood of the object is actually warped. Thus we can either talk in terms of masses [as we normally do] or in terms of local curvatures of space-time [when we use Einstein’s theory]. Take first a good look at the figure below.

Figure 1: Shown here via a two dimensional grid is the concept of space-time warp. According to Einstein’s theory of general relativity, space remains unwarped when empty, that is free from matter. However, when matter is present, space gets warped. Although we have illustrated the idea here with a two-dimensional drawing, we must remember that our space is really three-dimensional. The point is just this: Matter distorts space. In fact, one can even say that matter is just a “hump” or may be a “dimple” in space! Professor Wheel describes the relationship between space warp and matter in an interesting way. He says: “Matter tells spacetime how to curve, and spacetime tells matter how to move!”

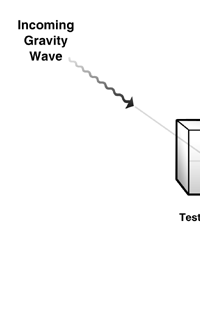
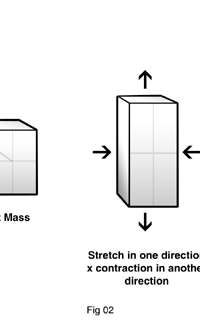
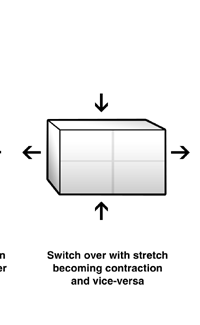
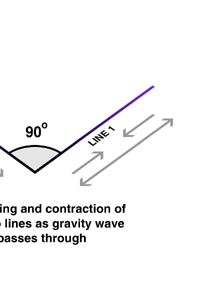
The above figure tells us if there is a mass, m say, then space-time in its neighbourhood gets warped. Suppose the mass m is moved; what happens to the curvature in space-time that I just mentioned? What happens is similar to what happens when we take a paddle and stir up water in a lake. The effect of the stir would propagate as a disturbance on the surface of the water and reach other spots. Suppose we have a piece of cork on the water surface some distance away. When the disturbance reaches the cork, it would start going up and down, indicating to us that it is experiencing the passage of the wave in its neighbourhood. The same thing happens when a mass is moved in space-time.

It generates a gravitational wave that moves at the speed of light. And when this wave encounters another mass [that I shall call the test mass], it would disturb the curvature of space-time associated with the test mass. In practical terms, the test mass would experience a distortion in its shape. In particular, in one direction perpendicular to the direction of the wave it would get squeezed, while simultaneously experiencing an elongation in the perpendicular direction. A little later, the squeeze would be replaced by elongation while the elongation would be replaced by a squeeze. In other words, there would periodic distortions of the shape of the test mass, the frequency being that of the gravitational wave. See Figure 2. By the way, these frequencies are generally quite low, ranging from about 1000 cycles/sec to as low as 10^-4 cycles/sec.

FIGURE 2: This figure shows how a mass gets distorted when impacted by a gravity wave. Basically the gravity wave stretches the object in one direction while contracting it at the same time in a perpendicular direction. This is done periodically, that is to say stretch-contract is followed by contract-stretch which is followed by a repeat of stretch-contract and so on. In other words, the mass shape of the mass undergoes oscillations. To detect a gravity wave, one must basically detect these oscillations of distortion. The problem is that these oscillations are incredibly small – that is where the problem is!

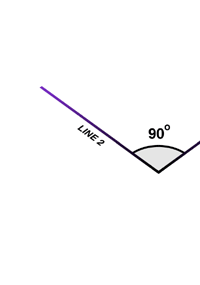
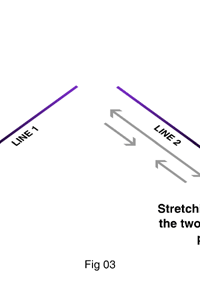
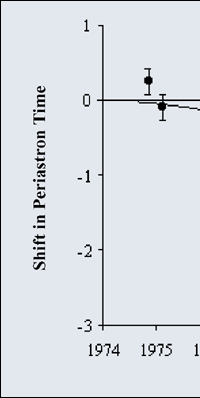
Searching for the Elusive Gravity Wave

What it all boils down to is that if we want to detect a gravitational wave, we should be able to detect low frequency distortions of say a large metallic object, say a cylinder. The problem is that the distortions are extremely small. How small? Well, about the size of an atomic nucleus! That’s tough, and that is why gravitational waves have not been detected thus far. This does not mean no one has tried. It has been, and a bit of that story is narrated in BOX 1.

Alright, so no one has detected a gravitational wave, but is there any evidence for it, even if say a bit indirect? There sure is and a pretty spectacular one too, one that in fact fetched two people the Nobel Prize! That story is told in BOX 2. What we learn from these two boxes is that 1) terrestrial detection of gravity waves is a tough job, 2) that said, there is clear [indirect] evidence that gravity waves do exist, and technology having made vast leaps, there is a lot of incentive to kick start gravitational astronomy.

The proponents of gravitational astronomy argue, “Currently, the gravitational-wave ‘sky’ is entirely unexplored. Since many prospective gravitational wave sources have no corresponding electromagnetic signature (e.g., black hole interactions), there are good reasons to believe that the gravitational-wave sky will be substantially different from the electromagnetic one. Mapping the gravitational-wave sky will provide an understanding of the Universe in a way that electromagnetic observations cannot. As a new field of astrophysics, it is quite likely that gravitational wave observations will uncover new classes of sources not anticipated in our current thinking.” Since detecting gravity waves is a tough job, gravitational astronomy does not come cheap; so the supporters have had to compete hard to get some funding, and finally, a start has been made.

Many projects have been planned and are currently in various stages of implementation; understandably, the biggest of them is in America, It is called LIGO, standing for Laser Interferometric Gravitational Observatory, and the principle involved can be understood by consulting Fig. 3 below. The basic idea is this; Imagine drawing two long straight lines on the surface of the earth, lines that are exactly perpendicular to each other, and intersect at a point. Suppose a gravity wave passes through that region. If you recall an earlier remark that the passage of gravity waves essentially makes space-time itself to go into oscillation, then it is easy to understand that the space-time associated with these two lines would contract and stretch as in the Fig. 3. What Joseph Weber tried to do [BOX 1] was to have a large aluminium bar and see how it responded to the warps in space-time [recall Fig.2]. The new idea was to get rid of the bar altogether and use space-time itself.

FIGURE 3: This schematic helps us to understand the basic idea underlying the LIGO. Imagine two long straight lines on the surface of the earth. When a gravity wave passes through this region, this part of space would get periodically warped. If one can somehow pick up those oscillatory warps, then one would have a way of detecting gravity waves. As explained in the text, an old trick of optics is used to pick up those oscillating space warps.

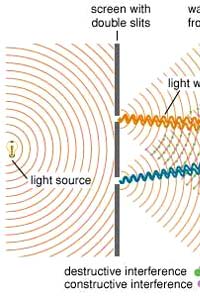
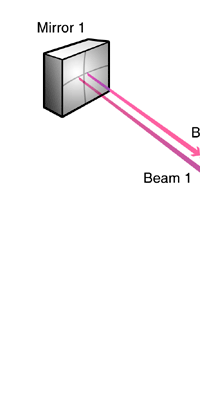
Now you may ask: “OK, gravity waves make the space along the two lines oscillate as the result of the contraction and expansion they produce. So what? No one can see space; so what’s the use?” Ah, that’s where human ingenuity comes into the picture. You see for about three hundred years at least, people have learnt to inter-compare distances using light beams. The way this works is explained in Fig. 4.

FIGURE 4: This figure shows how two light beams can interfere to produce a interference pattern.

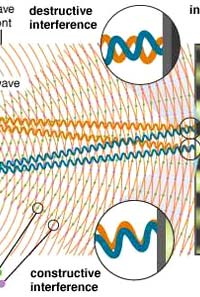
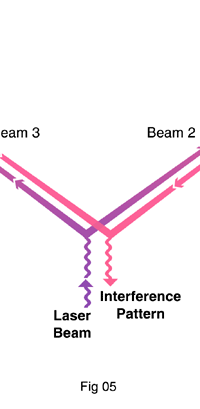
Gravitational astronomers said: “We will split a laser beam into two beams, make one go along one path and the other one along the other. At the end of the paths, we would put mirrors, so that the two beams get reflected and return to the starting point. There, we would try to see whether they arrive at the same time or at different times. How? Via interference fringes. The idea is illustrated in Fig. 5

FIGURE 5: This figure gives an idea of the principle behind the LIGO. Basically light from a laser is split into two beams and sent along two perpendicular directions for say about 4 km or so. At the end of the path, there are mirrors which reflect the beams back. The beams return, interfere and produce a fringe system. If a gravity wave passes through, the fringe system would be set into oscillations. The task now is to detect these oscillations.

The problem is that even when there is no gravity wave, the fringe system would wobble due to all sorts of terrestrial disturbances. Riding on top of all these would be the space-time quakes, and the problem is to detect these. Researchers said, “We think we can do it, and so give us the money!” The campaigners have succeeded and managed to get some money to do some proof of concept experiments. Two LIGO labs have been established and they are located at Hanford, Washington and Livingston, Louisiana. The work of these labs would involve two phases, an initial phase and an advanced phase.

Two Massive Labs to Detect the Waves

LIGO Hanford Observatory (LHO), located on the U.S. Department of Energy Hanford site in eastern Washington, comprises 5 major experimental halls for the interferometer spread over 5 miles. 1.2 m diameter ultrahigh vacuum tubing connects these halls. Three support buildings house laboratories, offices, and an amphitheater, and two additional buildings are associated with maintenance and operations. Approximately 90,000 square feet of this space is under tight environmental control to minimize contamination of sensitive equipment. The physical plant has been designed to provide a low vibration environment similar to the surrounding undeveloped shrub-steppe environment.

LHO houses two interferometers with arm lengths of 4 km and 2 km. The 4 km equipment is installed in vacuum chambers in the corner station and the two end stations on each arm. The 2 km equipment uses vacuum chambers in the corner station and the two mid-stations situated halfway down each arm. The two interferometers share 2 km of beam tube along each arm. The beam tube can eventually accommodate up to 5 interferometer beams and the current station buildings can accommodate up to 3 interferometers to accommodate future growth.

Aerial view of LHO

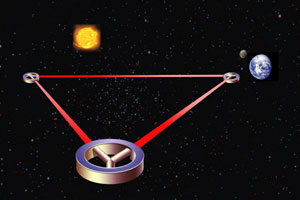
The LIGO Livingston Observatory, located in pine forests between Baton Rouge and New Orleans, Louisiana, is the site of a single 4 km laser interferometer gravitational wave detector. Construction of its physical facilities, scaled to accommodate one interferometer, is complete. The beam tube dimensions are identical to those at LHO.

I must now make a few remarks to indicate how tough these experiments are. Gravity waves being weak, the wobbles that one is looking for in the interference pattern would also be very tiny. Hence, one must take all the precaution one can to keep confusing signals to a rock bottom, and that is where most of the money gets spent. This is called achieving a high signal-to-noise ratio, and boy does achieving a high ratio swallow money?!

Where do these disturbing signals come from? From many sources; if the light path is in air, then the air molecules can cause problems, and so one has to have a vacuum tube all along the light path, as you can see in the photo above. The laser beam can fluctuate and that could mean problems. Small seismic disturbances can disturb the reflecting mirrors which mean more problems, which is why these labs are located in remote places to the extent possible.

The instruments that are being installed to get going are called Initial LIGO, to be soon followed by what is called Advanced LIGO, which would enhance detection sensitivity by more than a factor of 10 over the entire initial range of frequencies that LIGO would operate in. Just to give you an idea of what that means, what Initial LIGO would be able to achieve during one whole year would get done by the advanced machine in a few hours.

I should add that though the LIGO labs are located in America, the US has opened the door for international collaboration, via what is called LIGO Scientific Collaboration [LSC]. LSC includes scientists from India, Russia, Germany, U.K., Japan and Australia. The international partners are involved in all aspects of the LIGO research program. Initial LIGO would start operations in 2009. By 2011, installation of Advanced LIGO would commence even while the Initial LIGO would slowly be decommissioned.

Outer Space Makes for Better Experimental Conditions

OK, so what must one do to make gravity wave detection even more sensitive. The first and the most obvious thing to do is to increase the length of the arm of the interferometer. But then, due to the curvature of the earth, we cannot go too far in that direction. If we want to increase the length, then there is only way to do it, go into space! And that has given birth to the idea called Laser Interferometer Space Antenna, known better as LISA. In a sense, LISA is like LIGO, with two interferometric arms. However, the arms are out in space.

Here's how it works: A laser beam from one of the spacecraft is pointed toward a detector on another spacecraft, 5 million kilometers away. The laser beam precisely measures a distance between the two spacecraft. When the distance changes, an interference pattern is formed, and LISA has detected a gravitational wave. The three arms of the spacecraft work together to confirm each other's observations, as well as to get more detailed information about the passing waveform.

LISA can measure a change in length approximately 1000 times smaller than the diameter of an atom (or about 30 times the size of the nucleus of an atom!). To measure the very small strains expected for gravitational waves, the distance between spacecraft must be very large - about 5 million km. This is approximately 13 times the distance between the earth and the moon. This observatory will be very sensitive!

Schematic of LISA		Schematic of LISA's Orbit
LISA going round the Sun

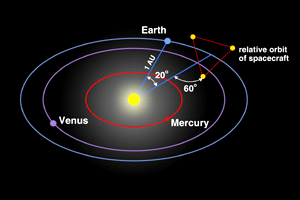
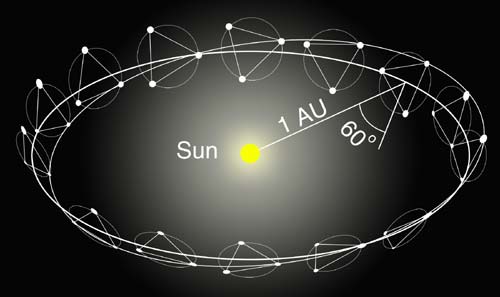
The two detectors (LIGO and LISA) complement each other because they cover different frequency ranges. (See illustration below.) Ground-based detectors cannot see very low frequencies because the ground moves too much (remember - these detectors can see motions that are smaller than the size of atoms). A space-based detector that is free from the motion of the earth is the only way to see low frequencies.

According to the current concept, the three identical LISA spacecraft will be launched together on a single Atlas V launcher. They will then independently reach their final orbits around the Sun using their propulsion modules that will be jettisoned prior to starting the scientific operations. The three spacecraft will be located at the vertices of a triangle, with an arm’s length of 5 million kilometres. The orbits will be similar to that of the Earth, but will trail our planet by approximately 50 million kilometres.

It will take one year for the three spacecraft to reach their final position and to start the actual mission. The LISA triangle will face the Sun, at an angle of 60 degrees to the plane of Earth's orbit, revolving with Earth around the Sun.

These heliocentric orbits for the three spacecraft were chosen so that the triangular formation is maintained throughout the year, with the triangle appearing to rotate about the centre of the formation once per year. The relative movement of the three spacecraft will help to detect the direction of each source and to reveal the nature of the gravitational waves.

The distance between the spacecraft determines the frequency range in which LISA can make observations; it has been carefully chosen to allow observation of most of the interesting sources of gravitational radiation, namely massive black holes and binary stars.

This plot shows the range of gravitational wave amplitiudes and frequencies that LISA and LIGO will be sensitive to. Shaded areas show the frequency and amplituded of gravitational waves given off by different types of objects. (NS = Neutron Star, BH = Black Hole, SN = Supernova Remnant.)

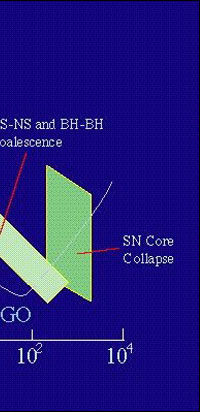
This figure to which I referred earlier, shows the frequency ranges in which LIGO and LISA operate. As you can see, the frequency bands are very different, and the kind of phenomena that can be studied are also different. In short, the two machines would complement each other. Right now, LISA is a concept, and one must see if it would get the funding required to get built and launched! Even it is, I do not know if it can help in getting answers related to the early Universe. However, it would teach us how to do advanced gravitational astronomy, and that in due course, would lead on to more sensitive and sophisticated astronomy – that is the way astronomy has always marched forward.

OK, it is clear we must use gravitational astronomy if we are to get answers to some tough questions relating to the very early history of our Universe, particularly regarding the question whether there was inflation as many say there was, or whether our Universe was born according to the script given by the Ekpyrotic Model. The big question now is: “Will gravitational astronomy ever reach that stage as to give us some definitive answers?” My response is: “If the question is whether technology can ever rise to that level and whether humans can ever rise to that level of excellence, the answer if a clear yes. However, there is a big IF!”

The Big ‘Ifs’ of Funding

IF? Why is that? Well, it all depends upon where humanity would be in say fifty years from now. In my lifetime, I have seen between the fifties and the nineties, progress no one, and I mean no one could have forecast way back in 1955, for instance. Technology reached amazing heights, and thanks to it, impossible feats got done. But since then, we have also been getting very strong signals that those sunny days could become dreams of the past.

It all boils down to a few basic issues which include the following:

A few comments now on all these issues combined. In the period from the fifties to the nineties, funds for basic research simply flowed, thanks to the huge support received by the scientific community in America. In this sense, America set the pace and others followed. In those days, there were not many competing priorities for the simple reason that in fields like biology, for example, there were no mega projects like one saw in Physics. But soon, there came projects like the Human Genome Project which demanded substantial funding.

Meanwhile many social problems began to become acute, and politicians in America who once tried to outdo each other in the matter of voting for funds for basic research, now began to have second thoughts – after all, they had to survive and for that, the vote bank was important. Just to illustrate the point, I might mention that in the eighties, physicists in America dreamed up a huge accelerator project called the Superconducting Super Collider [SSC for short]. It was to be the world’s biggest accelerator, and thanks to the huge campaign [in which the political angle was duly played up, meaning how America could not afford to be second to Europe], funds were voted not only for doing various preliminary studies but for actually going ahead with the project.

The giant machine was due to come up in Texas, and the machine as conceived was MUCH bigger than the machine now getting ready to operate in Geneva. Construction work actually started but then came the issue of competing priorities. Many in the US felt, “What is the big idea of spending billions of dollars for finding out something that might be very exciting for a few hundred physicists may be when we desperately need dollars for providing healthcare benefits for the poor?"

I still remember seeing in 1990 on America TV [when I was briefly in that country on some work] an old man appearing and saying with a long drawl, “I don’t know what these scientists want to spend so much on finding out something which nobody can understand, when there is no money to take care of old people like me? Will somebody explain to me why our tax dollars should be spent to make these scientists happy, abandoning at the same time old folks like me?”

I suppose you get the idea. By the way, while social activists were waging their campaign, there was a lot of sniping from within the scientific community itself, including from within the Physics community! I know how many solid state physicists were bitter about the way funds were cut from their programs for diversion to high energy physics. That should give some idea of competing priorities. These days, there are additional items on the list of priorities, like the so-called war on terror, etc.

There is more to this. The kind of projects I described would require launches of many satellites into space. About seventy percent at least of this funding has to come from America, which means NASA [National Aeronautic and Space Administration] must get the funding for it; Europe, Russia, and Japan might pitch in with the balance, perhaps. But right now, the NASA budget is very tight, and within that organisation, there are many competing priorities. There are some who want more of human exploration of the Moon followed by a Mars landing by humans. Then there are all kinds of satellite experiments that astronomers want flown. Then are people who want money for more development on the technology side. Among this fairly large group of competitors, would be the group that wants satellites for gravitational astronomy.

If you ask me, based on various current problems facing humanity, I doubt very much if the kind of astronomy that is called for to decide issues relating to inflation vs. Ekpyrotic model does stands much chance of getting funding for a long time. So maybe, we would not know the answer via experiments. However, there is a chance that good computer models might emerge, whose predictions could be tested via other experimental methods that are less costly. That said, direct confirmation by observing gravitational signatures would take a long, long time.

That’s all for this issue and next time we are going to take a sharp turn. Where would that take us? Join me again next month to find out!

	BOX 1 When Newton discovered the Law of Gravitation, the question arose: Suppose a mass m1 is separated from another m2 by distance r; suppose the distance r is increased by a small amount, by moving the mass m1 further away from m2. How would mass m2 know about this increase of separation, and how long would it be before m2 becomes aware of the change of separation? It was argued in those days that the transmission of information about the movement of m2 would be instantaneous. This was called the Principle of Action at a Distance. However, when it became clear from Einstein’s Special Theory of Relativity [developed in 1905] that information could NOT travel faster than the speed of light, the Principle of Action at a Distance got automatically ruled out. So what next? Well, Maxwell’s Electromagnetic Theory gave a hint about the way out. And Einstein took the hint and in 1915 came up his Theory of General Relativity, which allowed gravitation also to be described in terms of a field, very similar to what is done in Maxwell’s theory. And even as Maxwell described the transmission of electromagnetic information from one point to another via electromagnetic waves, Einstein stated that gravitational information too is transmitted in terms of gravitational waves, which travel at the speed of light. So, there was no more any need for the Principle of Action at a Distance. Joseph Weber   That was fine, but what about experimental evidence for gravitational waves? Well, one of the earliest attempts to detect such disturbances was made by Joseph Weber of the University of Maryland in College Park. Weber used solid aluminium cylinders, about 2 meters long and 1 meter in diameter, and suspended them on steel wires. A passing gravitational wave would set one of these cylinders vibrating at its resonant frequency--about 1660 hertz--and piezoelectric crystals firmly attached around the cylinder's waist would convert that ringing into an electrical signal. Weber took great pains to isolate the cylinders from vibration and from local seismic and electromagnetic disturbances, and claimed that the only significant source of background noise came from random thermal motion of the aluminium atoms. On account of this random thermal motions, the cylinder's length was expected to vary erratically by about 10-16 meters, less than a proton's diameter. This might seem very small but the expected gravitational wave signal was not much bigger. So basically, Weber was trying a very difficult experiment. Eventually, Weber looked for bumps in the data that exceeded some "threshold" that he characterized the background noise; however, he did not define this threshold consistently or precisely. Weber's used two bars and looked for signals in both bars within the same half-second period. His argument was that if the same signal is seen in both bars it was a genuine signal and not a random bump seen simultaneously in both bars by sheer accident. After seeing some coincident events between two Maryland bars, Weber moved one of his cylinders to Argonne National Laboratory, near Chicago, about 1000 kilometers away. In 1969 he published a paper reporting about two dozen coincident detections at the two locations in an 81-day period. He calculated that some of the signals were so large that coincidences by chance should happen only once in hundreds or thousands of years. This was "good evidence" for gravitational waves, he argued. The following year he claimed to have detected 311 coincident signals in a 7 month period, with a directional concentration, moreover, pointing toward the centre of the Milky Way. The second announcement in particular created a stir and many groups decided to repeat Weber’s experiments. However, none of these groups ever saw anything but random noise. People then began to analyse in detail why Weber alone saw signals that no one else saw. It was finally concluded that Weber being an electrical engineer who entered physics later in his career, did not know enough about rigorous data analysis and statistical evaluation. As Tyson, one of those who repeated Weber’s experiment says, “Inadequate controls and lack of rigour in data analysis turned out to be Weber’s downfall." By the late 1970s, everyone but Weber agreed that his claimed detections were spurious. While Weber was proved wrong no doubt, physicists now got hooked on gravity wave detection. In that respects, says Tyson, Weber deserves credit for drawing others into this field of physics, adding, "It was the difficulty that attracted us."

	BOX 2 As I have mentioned elsewhere, there is plenty of evidence for the correctness of Einstein’s Theory of General Relativity [see, for example, QFI 05]. However, direct detection of gravitational waves has been something of a quest for the Holy Grail. Detection of gravity waves involves detecting signals that are extremely feeble and could be easily masked. So, it basically boils down to a signal-to-noise ratio problem, or to use a popular phrase, a problem similar to searching for a needle in a haystack. In 1974, Russell Hulse and Joseph Taylor of Princeton University detected a pulsar designated PSR 1913+16. It was one member of a binary system; that meant the pulsar had a companion star, and the two were orbiting around a common centre of mass. In this case, the companion was not visible. Prolonged measurements made on the pulsar showed that the orbital period of the pulsar [that is, the time for it to complete an orbit (about eight hours)] was steadily decreasing. The decrease was extremely small being about 0.000414 seconds in four years! What amazing accuracy!! The question then became: Why this decrease? The widely accepted explanation is that the binary system is losing energy through the emission of gravitational waves, causing the two stars to slowly spiral towards each other. This spiralling in turn would cause a decrease of the orbital period of the pulsar. In 1993, Hulse and Taylor were awarded the Nobel Prize in Physics for their discovery. At present, no one is doubting the existence of gravitational waves; but then, there is nothing like actually detecting them! For the benefit of the more curious, I offer below some more details, throwing more light on what exactly Hulse and Taylor did. The first thing I would like to mention is that the pulsar detected by Hulsa and Taylor was quite unusual – it was spinning rather fast compared to all pulsars known earlier; it was rotating about its axis 17 times per second, and thus its radio pulses were coming quite fast, at the rate of once every few milliseconds. For this reason, this pulsar was often called the millisecond pulsar. Now until then, all pulsars were known to maintain their periodicity to a high degree of accuracy. However, in this case, Hulse and Taylor noticed that there was a systematic variation in the arrival of the pulses. Sometimes, the pulses arrived a little sooner than expected while at other times, they arrive a bit later than they were supposed to. These variations occurred in a smooth manner and repeated every 7.75 hours. This gave them the clue that their pulsar was a member of a binary star. Binary stars are quite well-known in astronomy; basically, they are a pair of stars each of which moves in an elliptic orbit around a common centre of mass, as shown in the figure below. As you can see from the figure, the orbits are quite eccentric. The minimum separation is about 1.1 solar radius, and the position at which this occurs is called periastron. There is similarly a maximum separation which occurs at apastron, the separation being about 4.8 times the radius of our Sun. In the case of PSR 1913+16, the orbit is inclined at about 45 degrees with respect to the plane of the sky, and it is oriented such that periastron occurs nearly perpendicular to our line of sight. FIGURE 1: This figure shows schematically how a pair of stars forming a binary perform a celestial and rhythmic dance of their own. Their special positions described in the text are also identified. The blue arrows indicate the directions of motion of the two stars in their various positions. The famous laws that Kepler discovered many centuries ago tell us that a celestial object would move slower when it is at apastron than when it is at perastron. The more the eccentricity of the orbit, the greater is the difference in velocity between these two positions. In the case of the pulsar PSR 1913+16, the velocity varies from a minimum of 75 km/sec to a maximum of 300 km/sec. By carefully studying the rate at which the pulses were arriving, Hulse and Taylor were able, to start with, infer all the details of the orbital motion of both the stars in the binary. The following figure illustrates how one might infer the size of the orbit in a simple case. Suppose one had a pulsar with no companion star; as you can see from the figure, during its orbital motion, the pulsar is sometimes closer to the earth while at other times, it is farther away from the earth. Thus, when the pulsar is closer, its pulses would arrive earlier, while when it is far away, the pulses would be slightly delayed. By studying the time difference, one can get a good idea of the size of the orbit. In the case of a binary star, one has to get the picture of both the orbits, by getting information from just one member; that is a bit more involved, but can be and is in fact regularly done. The next two figures throw more light on how features related to the orbit are deduced from experimental data. FIGURE 2: As is evident from the figure, the pulses take less time to arrive at the earth when the pulsar is at one end as compared to the other. From this, one can infer the size of the orbit. The exercise is relatively easy when the pulsar is all by itself; however, when it forms part of a binary, unravelling the orbital details becomes more involved; but it can be done, as it was in this case.   FIGURE 3: This figure shows actual data, namely the pulse frequency as a function of time. There are many features to be noted here. The first is that negative velocities, [that is, the velocity when the pulsar is approaching the earth] are larger than positive velocities [velocities when the pulsar is moving away from the earth]. This means the orbit is highly eccentric. Notice also that the pattern repeats every 7.75 hours. FIGURE 4: While the previous figure showed data with respect to pulse frequencies, this figure shows data with respect to pulse arrival times. The pulsar arrival times also vary as the pulsar moves through its orbit. When the pulsar is on the side of its orbit closest to the Earth, the pulses arrive more than 3 seconds earlier than they do when it is on the side furthest from the Earth. The difference is caused by the shorter distance from Earth to the pulsar when it is on the close side of its orbit. The difference of 3 light seconds implies that the orbit is about 1 million kilometers across. Thus, by combining the data of the various figures one not only gets an idea of the shape but also the size of the orbits. FIGURE 5: The orbit of the pulsar appears to rotate with time; in the diagram, notice that the orbit is not a closed ellipse, but a continuous elliptical arc whose point of closest approach ( periastron) rotates with each orbit. The rotation of the pulsar's periastron is analogous to the advance of the perihelion of Mercury in its orbit. The observed advance for PSR 1913+16 is about 4.2 degrees per year; the pulsar's periastron advances in a single day by the same amount as Mercury's perihelion advances in a century. Now the radio pulses coming from the pulsar are like the ticks of a clock. Hulse and Taylor realised that they could look for changes in the pulse rate caused by relativistic effects. Einstein’s Theory of General Relativity predicts that due to changing warps in space-time associated with the motion of the members of the binary, the system would lose energy which would get converted into gravitational radiation. When the system systematically loses energy, the orbit also shrinks. In practical terms, when the orbit shrinks, the pulses arrive earlier than they would if there was no shrinkage. The figure below shows data obtained by Hulse and Taylor, over a period of years. Clearly there is a systematic decrease, confirming that energy was being lost. Using Einstein’s theory, calculations were made and the observed shrinkage was fully consistent with what theory predicts. This means that there is really no doubt about the existence of gravitational waves; it was only a question of actually detecting them. FIGURE X: This figure shows the data obtained by Hulse and Taylor, clinching the argument for the existence of gravitational waves; the evidence, however, is indirect though very strong. As I mentioned above, the orbit of the pulsar is decreasing every year. The decrease is very small; during every orbit, the size shrinks by about 3.1 mm. But then this adds up over time and in about three hundred million years, the two members of the binary would collide. That collision would be a mega event, which would sure generate huge celestial gravitational “tsunami”. The kind of gravitational waves that would be generated would be strong enough to be detected by gravitational detectors now under construction. FIGURE C: This shows the orbit of the pulsar as it is now; for comparison, the Sun is also depicted. As a result of loss of energy due to relativistic effects, the orbit steadily shrinks, bringing the pulsar closer and closer to its companion. In about 300 million years from now, the two stars forming the binary would collide and maybe merge, generating a “gravitational tsunami”.

 

---